Matrices y Determinantes

¡Bienvenid@ a matricesydeterminantes.com!

En esta web encontrarás toda la información acerca de las matrices y los determinantes, así como ejercicios resueltos paso a paso con los que podrás practicar. Hemos explicado cada tema al detalle para que se entienda todo al máximo posible, ¡pero si te queda alguna duda no dudes en escribirla en los comentarios! La resolveremos con mucho gusto. Solo tenemos un objetivo: ¡que consigas la mejor nota de la clase! 😉😘

Haz clic en el tema que más te interese:

¿Qué es una matriz?

En matemáticas, una matriz es una tabla de números que sirve para representar datos de manera ordenada.

La principal utilidad de las matrices es representar los datos de los problemas. Por ejemplo, una empresa que vende 3 productos (X, Y, Z) ha realizado un estudio de mercado para saber a qué precio venden estos productos sus principales competidores (M y N) y ha obtenido los siguientes datos:

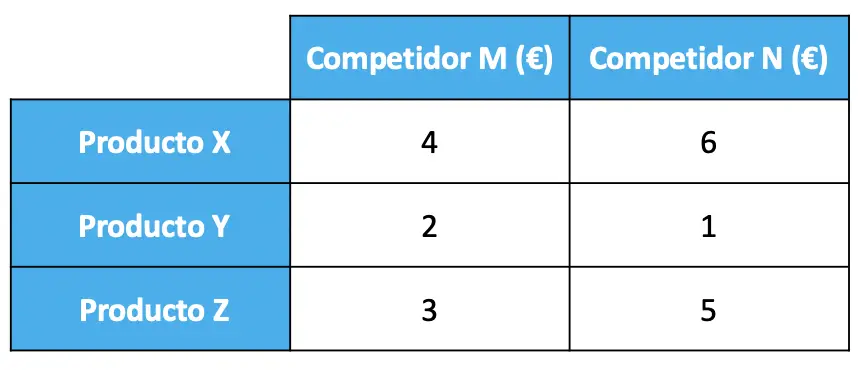
Pues la información de este problema se puede expresar en forma de matriz:

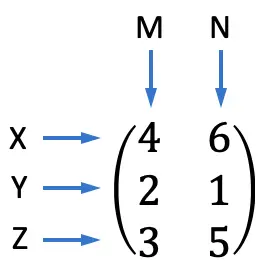
De esta forma se puede analizar mejor el problema y es más fácil de resolverlo. Para ver cómo calcular la solución de un sistema matricial puedes consultar el link del principio de la página.

En este caso concreto, hemos obtenido una matriz rectangular de 3 filas y 2 columnas. Para abreviar se suele decir que es una matriz de dimensión 3×2.

¿Qué es el determinante de una matriz?

El determinante de una matriz es una operación que se aplica a las matrices, pero únicamente se pueden calcular los determinantes de matrices cuadradas. Por lo tanto, el resultado del determinante de una matriz siempre será un número, no una matriz. Por ejemplo, el determinante de la siguiente matriz es igual a cero (0):

Si quieres saber cómo resolver el determinante de cualquier matriz haz click en el link del principio de la página.

Como puedes ver, los determinantes siempre se expresan con barras verticales, a diferencia de las matrices que normalmente se representan con paréntesis.

¿Cuál es la diferencia entre una matriz y un determinante?

La principal diferencia entre las matrices y los determinantes es que una matriz es una manera de expresar datos o números, en cambio, el determinante de una matriz siempre será el resultado de una operación, es decir, un único número.

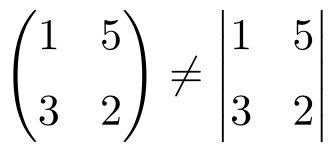
Otra manera de diferenciar las matrices y los determinantes es mediante sus respectivas propiedades. Por ejemplo, multiplicar una matriz por un número es equivalente a multiplicar todos los elementos de la matriz por ese número. Por contra, el producto de un determinante por un escalar es igual a multiplicar tan solo una fila o una columna del determinante.

Otra propiedad en la que se diferencian las matrices y los determinantes es en la multiplicación entre sí. Porque en general las matrices no son conmutables, es decir, el resultado del producto entre dos matrices varia dependiendo del orden en el que se multiplican. Por el contrario, el producto entre dos determinantes sí que es conmutativo.

Siendo y dos matrices diferentes y y sus respectivos determinantes.

Historia de las matrices y de los determinantes

Es difícil decir exactamente cuándo y dónde se inventaron las matrices y los determinantes, ya que se usan desde hace mucho tiempo. Sin embargo, seguramente el origen de las matrices se encuentra en China hacia el año 650 a.C., donde se utilizaban las matrices para estudiar los cuadrados mágicos.

Asimismo, hay constancia de que también se usaban las matrices para resolver sistemas de ecuaciones lineales en un importante texto matemático chino (Nueve capítulos sobre el Arte de las matemáticas, Jiu Zhang Suan Shu) que proviene del año 300 a.C. al 200 a.C. En ese documento se explica un método matricial para hallar la solución de sistemas con 3 ecuaciones y 3 incógnitas.

Además, los cuadrados mágicos también eran conocidos por los matemáticos árabes probablemente desde el principio del siglo VII, quienes podrían haberlos adquirido a través de los matemáticos y astrónomos de India. Todo esto sugiere que el concepto proviene del territorio chino.

Por otro lado, aunque el término de determinante ya aparecía por primera vez en el escrito chino del siglo III a.C., el matemático japonés Seki Kōwa hizo una publicación en 1683 sobre el cálculo de determinantes. Más tarde, en 1693, el famoso matemático alemán Leibniz contribuyó al desarrollo de la teoría de los determinantes con un método para resolver sistemas de 3 ecuaciones y 2 incógnitas.

Más adelante, el matemático escocés Maclaurin aportó un método para resolver sistemas de ecuaciones lineales con 2, 3 y 4 incógnitas. Esta obra se publicó en 1748, pero se piensa que ya utilizaba este método por el año 1729. No obstante, fue en 1750 cuando el suizo Gabriel Cramer encontró la fórmula para solucionar un sistema de cualquier dimensión con el mismo número de incógnitas que de ecuaciones (n×n) mediante determinantes. Este método aún se usa actualmente bajo el nombre de la regla de Cramer.

El francés Bezout también hizo importantes contribuciones en este campo del álgebra lineal. Por ejemplo, en 1764 demostró que existen soluciones no nulas en un sistema homogéneo de n ecuaciones lineales con n incógnitas si el determinante asociado a los coeficientes del sistema se anula.

A finales del siglo XVIII el brillante matemático francés Laplace aportó estudios relevantes a la teoría sobre las matrices y los determinantes. Entre ellos destaca un procedimiento para resolver cualquier determinante, conocido como la resolución de un determinante por adjuntos o cofactores, o incluso la regla de Laplace.

A parte, durante ese periodo los científicos Euler y Newton investigaron sobre la aplicación de los determinantes para calcular las raíces de polinomios, pero sus resultados nunca llegaron a expandirse tanto como otros métodos.

En el siglo XIX los matemáticos Carl Friedrich Gauss y Wilhelm Jordan desarrollaron otro método para determinar la solución de sistemas de ecuaciones lineales. Este método se llama método de Gauss-Jordan y consiste en transformar la matriz asociada al sistema en una matriz escalonada. Este método es muy importante y, de hecho, actualmente se utiliza bastante y suele preguntarse en la selectividad con frecuencia.

En el año 1833 el matemático Pierre Frédéric Sarrus publicó un artículo en el que se explicaba una técnica mnemotécnica para calcular el determinante de una matriz 3×3: la regla de Sarrus.

A pesar de que ya se utilizaban antes, hacia los años 1848-1850 fue el inglés James Joseph Sylvester quien se inventó el término de «matriz» para nombrar a este tipo de expresiones matemáticas.

Durante esa etapa también hay que resaltar la contribución del célebre matemático francés Cauchy a la teoría sobre matrices y determinantes. Entre sus trabajos destaca que él probó el teorema de la multiplicación de matrices y desarrolló gran parte de la diagonalización de matrices, como los valores propios (o autovalores) y vectores propios (o autovectores) o demostrar que toda matriz simétrica real es diagonalizable.

Otro matemático que aportó grandes avances en el álgebra matricial fue el británico Arthur Cayley. Por ejemplo, él definió la igualdad de matrices, la matriz nula, la suma y la resta de matrices, etc. Pero sobre todo destaca por definir las matrices invertibles. De hecho, incluso existe un teorema que lleva su nombre, el teorema de Cayley-Hamilton, que permite encontrar el polinomio característico de una matriz.

Por otra parte, a medianos del siglo XIX el alemán Jacob Jacobi dio otro sentido a los determinantes de matrices. Él empezó a utilizar los determinantes funcionales, o dicho de otra forma, determinantes que no solamente contienen números sino que también pueden estar formados por funciones, como por ejemplo la matriz Jacobiana y la matriz Hessiana.

En el año 1879 el alemán Frobenius introdujo el concepto de rango de una matriz. Por esa razón existe un teorema con su nombre, el teorema de Rouché – Frobenius, que permite distinguir qué tipo de sistema de ecuaciones se trata a través del rango de sus matrices asociadas. Además, Frobenius dio la definición de matriz ortogonal.

Finalmente, ya en pleno siglo XX, en el año 1925, Werner Hesenberg redescubre el cálculo matricial haciendo una primera formulación de lo que posteriormente sería la mecánica cuántica.

Otros extraordinarios matemáticos que también han contribuido al progreso de la teoría sobre matrices y determinantes han sido Olga Taussky-Tod, Herman Grassman, Karl Weierstraß y John von Neumann.

Aplicaciones de las matrices

Las matrices y los determinantes tienen muchas aplicaciones reales y, por eso mismo, se utilizan muy a menudo en la actualidad. Las principales razones por las que se usan las matrices son: para resolver problemas, para relacionar datos entre sí, y para hacer cálculos vectoriales.

Como hemos visto al principio, se puede representar un problema a través de una matriz, en cuyo caso decimos que es una matriz de información. Y, del mismo modo, se puede expresar un sistema de ecuaciones lineales mediante matrices:

En consecuencia, se pueden utilizar las matrices y los determinantes para resolver sistemas de ecuaciones lineales.

Por otro lado, también se usan las matrices para expresar las relaciones entre datos, estas son las llamadas matrices de información. Por ejemplo, es muy fácil hacer la representación de un grafo y de las relaciones que existen entre sus nodos mediante una matriz: si dos nodos están relacionados se pone un 1, en cambio, si no existe ninguna relación entre dos nodos se coloca un 0.

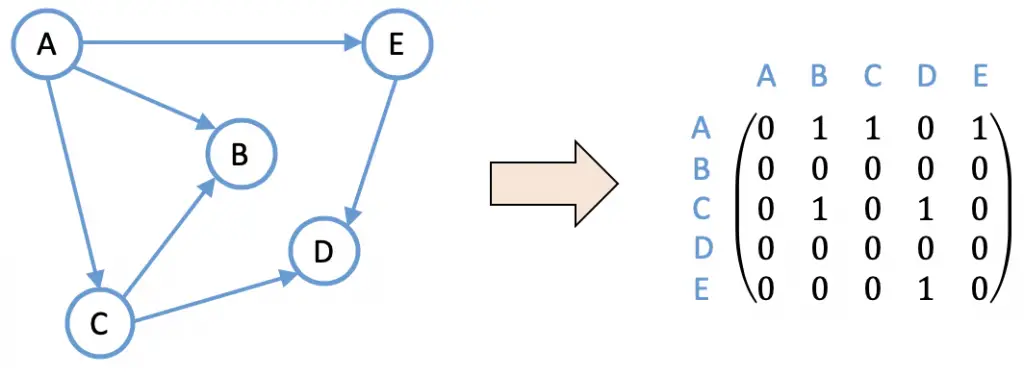
Por último, otra utilidad de las matrices es representar vectores. Se pueden usar las columnas de las matrices para expresar las coordenadas de un vector y hacer operaciones con ellos. Por ejemplo, si el determinante de una matriz es igual a 0 significa que el rango de la matriz en cuestión nunca será máximo, y esto implica que los vectores de la matriz serán linealmente dependientes (LD). Por contra, si el determinante es distinto de 0 los vectores son linealmente independientes (LI).