Todas las Propiedades de los Determinantes (con ejercicios)

En este apartado vamos a ver cuáles son todas las propiedades de los determinantes. También te demostramos cada propiedad con un ejemplo para que las entiendas a la perfección. Y, además, encontrarás ejercicios relacionados con las propiedades de los determinantes.

A continuación vamos a explicar una a una cada propiedad de los determinantes, pero si lo prefieres puedes ir directamente a la tabla resumen que hay más abajo. 😉

Sumario

1. Propiedad 1: Determinante de la matriz transpuesta

2. Propiedad 2: Determinante con una fila o columna llena de ceros

3. Propiedad 3: Determinante con dos filas o columnas iguales

4. Propiedad 4: Cambiar filas o columnas de un determinante

5. Propiedad 5: Multiplicar una línea de una determinante por un escalar

6. Propiedad 6: Determinante del producto matricial

7. Propiedad 7: Determinante de la matriz inversa

8. Propiedad 8: Sustituir la fila de un determinante

9. Propiedad 9: Determinante de una matriz triangular

10. Propiedad 10: Determinante de una matriz diagonal

11. Tabla resumen de las propiedades de los determinantes

12. Ejercicios resueltos con propiedades de los determinantes

Propiedad 1: Determinante de la matriz transpuesta

El determinante de una matriz es equivalente al determinante de su matriz traspuesta.

$\lvert A \rvert = \lvert A^t \rvert$

Ejemplo:

$\lvert A \rvert = \begin{vmatrix} 2 & 3 \\[1.1ex] 1 & 5 \end{vmatrix} = 2 \cdot 5 - 1 \cdot 3 = 10 - 3 = \bm{7}$

Ahora trasponemos la matriz 2×2 y resolvemos el determinante. Fíjate que obtenemos el mismo resultado que antes:

$\lvert A^t \rvert = \begin{vmatrix} 2 & 1 \\[1.1ex] 3 & 5 \end{vmatrix} = 2 \cdot 5 - 3 \cdot 1 = 10 - 3 = \bm{7}$

Propiedad 2: Determinante con una fila o columna llena de ceros

Si un determinante tiene una fila o una columna llena de ceros, el determinante da 0.

$\displaystyle \begin{vmatrix} a_{11} & 0 & a_{13} \\[1.1ex] a_{21} & 0 & a_{23} \\[1.1ex] a_{31} & 0 & a_{33}\end{vmatrix}=0$

Ejemplo:

$\begin{vmatrix} 5 & 6 & 2 \\[1.1ex] 0 & 0 & 0 \\[1.1ex] -3 & 1 & 4 \end{vmatrix} = \bm{0} \qquad \qquad \begin{vmatrix} 1 & -5 & 0 \\[1.1ex] 6 & 2 & 0 \\[1.1ex] 1 & 3 & 0 \end{vmatrix} = \bm{0}$

En estos dos ejemplos los determinantes dan como resultado 0. Porque la segunda fila del primer determinante es todo ceros y la tercera columna del segundo determinante también.

Propiedad 3: Determinante con dos filas o columnas iguales

Si un determinante tiene dos filas o dos columnas iguales o múltiples, el determinante es igual a cero (0).

Por lo tanto, si existe alguna combinación lineal entre filas o columnas, es decir son linealmente dependientes, el determinante da 0.

Ejemplo:

$\begin{vmatrix} 3 & 4 & 4 \\[1.1ex] -1 & 5 & 5 \\[1.1ex] 6 & 2 & 2 \end{vmatrix} = 0$

En este caso el determinante da 0 porque las columnas 2 y 3 son iguales.

Propiedad 4: Cambiar filas o columnas de un determinante

Si se cambian dos filas o dos columnas entre sí, el determinante da el mismo resultado pero cambiado de signo.

$\displaystyle \begin{vmatrix} a & b & c \\[1.1ex] d & e & f \\[1.1ex] g & h & i \end{vmatrix}= - \begin{vmatrix} a & c & b \\[1.1ex] d & f & e \\[1.1ex] g & i & h \end{vmatrix}$

Ejemplo:

$\begin{vmatrix} 3 & 2 & -4 \\[1.1ex] 1 & 5 & 6 \\[1.1ex] 1 & 0 & -3 \end{vmatrix} = \displaystyle -45 +12+0+20-0+6= \bm{-7}$

Ahora cambiamos de orden las columnas 2 y 3 entre sí. Fíjate que el resultado es el mismo pero cambiado de signo:

$\begin{vmatrix} 3 & -4 & 2 \\[1.1ex] 1 & 6 & 5 \\[1.1ex] 1 & -3 & 0 \end{vmatrix} = \displaystyle 0-20-6-12+45-0= \bm{+7}$

Propiedad 5: Multiplicar una línea de una determinante por un escalar

Multiplicar todos los elementos de toda una fila o de toda una columna por un número real, es igual a multiplicar el resultado del determinante por dicho número.

$\displaystyle \begin{vmatrix} k \cdot a_{11} & k \cdot a_{12} & k \cdot a_{13} \\[1.1ex] a_{21} & a_{22} & a_{23} \\[1.1ex] a_{31} & a_{32} & a_{33} \end{vmatrix} =k \cdot \begin{vmatrix} a_{11} & a_{12} & a_{13} \\[1.1ex] a_{21} & a_{22} & a_{23} \\[1.1ex] a_{31} & a_{32} & a_{33} \end{vmatrix}$

$\displaystyle \begin{vmatrix} k \cdot a_{11} & a_{12} & a_{13} \\[1.1ex] k \cdot a_{21} & a_{22} & a_{23} \\[1.1ex] k \cdot a_{31} & a_{32} & a_{33} \end{vmatrix} =k \cdot \begin{vmatrix} a_{11} & a_{12} & a_{13} \\[1.1ex] a_{21} & a_{22} & a_{23} \\[1.1ex] a_{31} & a_{32} & a_{33} \end{vmatrix}$

Ejemplo:

$\displaystyle \begin{vmatrix} 2 & 3 \\[1.1ex] 1 & 4 \end{vmatrix} = 8-3= \bm{5}$

Ahora cogemos el mismo determinante y multiplicamos toda una fila por 2. Verás que el resultado será el del determinante anterior pero multiplicado por 2, es decir 10:

$\displaystyle \begin{vmatrix} 2 \cdot 2 & 2 \cdot 3 \\[1.1ex] 1 & 4 \end{vmatrix} = \begin{vmatrix} 4 & 6 \\[1.1ex] 1 & 4 \end{vmatrix} = 16-6 =\bm{10}$

Propiedad 6: Determinante del producto matricial

El determinante del producto de dos matrices es igual al producto del determinante de cada matriz por separado.

$\displaystyle \lvert A \cdot B \rvert = \lvert A \rvert \cdot \lvert B \rvert$

Ejemplo:

Para demostrar esta propiedad de los determinantes, vamos a calcular de las dos maneras posibles el determinante de la multiplicación de las siguientes dos matrices:

$\displaystyle A= \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & 5 \end{pmatrix}\quad B=\begin{pmatrix} 4 & 2 \\[1.1ex] 1 & -1 \end{pmatrix}$

Primero haremos la multiplicación de las dos matrices, y luego calcularemos el determinante de la matriz resultante:

$\displaystyle \left| A \cdot B \right| =\left| \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & 5 \end{pmatrix} \cdot \begin{pmatrix} 4 & 2 \\[1.1ex] 1 & -1 \end{pmatrix}\right| = \left| \begin{pmatrix} 7 & -1 \\[1.1ex] 13 & -1 \end{pmatrix} \right| = -7 - (-13) = \bm{6}$

Ahora calculamos el determinante de cada matriz por separado, y luego multiplicamos los resultados:

$\displaystyle \lvert A \rvert \cdot \lvert B \rvert = \left| \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & 5 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} 4 & 2 \\[1.1ex] 1 & -1 \end{pmatrix}\right| = -1\cdot (-6)= \bm{6}$

Como ves, hacer primero el producto matricial y después el determinante da el mismo resultado que hacer primero el determinante de cada matriz y luego la multiplicación de los resultados.

Por otra parte, esta condición no se aplica para las operaciones sumas y restas, es decir, el determinante de la suma (o resta) de dos matrices no da el mismo resultado que sumar (o restar) los determinantes de dos matrices por separado.

Propiedad 7: Determinante de la matriz inversa

Si una matriz es invertible, el determinante de su inversa corresponde al inverso del determinante de la matriz original.

$\displaystyle \begin{vmatrix} A^{-1} \end{vmatrix} = \cfrac{1}{\lvert A \rvert}$

Ejemplo:

Vamos a verificar esta propiedad calculando primero la inversa de una matriz y luego resolviendo su determinante. Veremos que el resultado es equivalente a hallar el determinante de la matriz original e invertirlo.

De modo que invertimos la siguiente matriz y calculamos su determinante:

$\displaystyle A= \begin{pmatrix} 4 & 2 \\[1.1ex] 7 & 4 \end{pmatrix}$

$\displaystyle A^{-1}= \begin{pmatrix} 2 & -1 \\[1.1ex] -\frac{7}{2} & 2 \end{pmatrix}$

$\displaystyle \begin{vmatrix}A^{-1} \end{vmatrix}= \begin{vmatrix} 2 & -1 \\[1.1ex] -\frac{7}{2} & 2 \end{vmatrix} = 4-\cfrac{7}{2} =\cfrac{8}{2}-\cfrac{7}{2} = \cfrac{\bm{1}}{\bm{2}}$

Y ahora resolvemos el determinante de la matriz original y hacemos su inverso:

$\displaystyle \begin{vmatrix}A\end{vmatrix}= \begin{pmatrix} 4 & 2 \\[1.1ex] 7 & 4 \end{pmatrix}=16-14=2$

$\displaystyle \begin{vmatrix}A^{-1}\end{vmatrix}= \cfrac{\bm{1}}{\bm{2}}$

Como puedes apreciar, los resultados de ambas operaciones son idénticos. Por lo que queda demostrada la propiedad.

Propiedad 8: Sustituir la fila de un determinante

Se puede sustituir la fila de un determinante por la suma (o resta) de la misma fila más (o menos) otra fila multiplicada por un número.

Ejemplo:

Con el siguiente ejemplo vamos a comprobar esta propiedad. Primero vamos a calcular un determinante, luego operaremos en una fila del determinante y volveremos a calcular su resultado. Ya verás como obtenemos el mismo resultado en los dos casos.

Así pues, primero calculamos un determinante 3×3 con la regla de Sarrus:

$\begin{vmatrix} 2 & 1 & -1 \\[1.1ex] 3 & 0 & 1 \\[1.1ex] 0 & -3 & 6 \end{vmatrix} \displaystyle=0+0+9-0+6-18 = \bm{-3}$

Ahora a la fila 2 le sumamos la primera fila multiplicada por 2:

$\displaystyle \begin{vmatrix} 2 & 1 & -1 \\[1.1ex] 3 & 0 & 1 \\[1.1ex] 0 & -3 & 6 \end{vmatrix} \begin{matrix} \\[1.1ex] \xrightarrow{f_2 + 2f_1} \\[1.1ex] \ \end{matrix} \begin{vmatrix} 2 & 1 & -1 \\[1.1ex] 7 & 2 & -1 \\[1.1ex] 0 & -3 & 6 \end{vmatrix}$

Y resolvemos el determinante después de haber transformado una de sus filas:

$\displaystyle \begin{vmatrix} 2 & 1 & -1 \\[1.1ex] 7 & 2 & -1 \\[1.1ex] 0 & -3 & 6 \end{vmatrix} = 24+0+21-0-6-42=\bm{-3}$

En los dos casos el resultado ha sido -3. Así que queda demostrado que el resultado de un determinante no varia si se sustituye una fila por la suma de la misma fila más otra fila multiplicada por un número.

Propiedad 9: Determinante de una matriz triangular

El determinante de una matriz triangular es el producto de los elementos de su diagonal principal.

Ejemplo:

Vamos a resolver el determinante de la siguiente matriz triangular a modo de ejemplo:

$\begin{vmatrix} 2 & 3 & 5 \\[1.1ex] 0 & -1 & 7 \\[1.1ex] 0 & 0 & 4 \end{vmatrix} \displaystyle= 2 \cdot (-1) \cdot 4 = \bm{-8}$

Propiedad 10: Determinante de una matriz diagonal

El determinante de una matriz diagonal es igual a la multiplicación de los elementos de su diagonal principal.

Ejemplo:

Vamos a sacar el determinante de la siguiente matriz diagonal como ejemplo:

$\begin{vmatrix}5 & 0 & 0 \\[1.1ex] 0 & 3 & 0 \\[1.1ex] 0 & 0 & -2 \end{vmatrix} \displaystyle= 5 \cdot 3 \cdot (-2) = \bm{-30}$

Tabla resumen de las propiedades de los determinantes

Las propiedades de los determinantes explicadas se pueden resumir en la siguiente tabla:

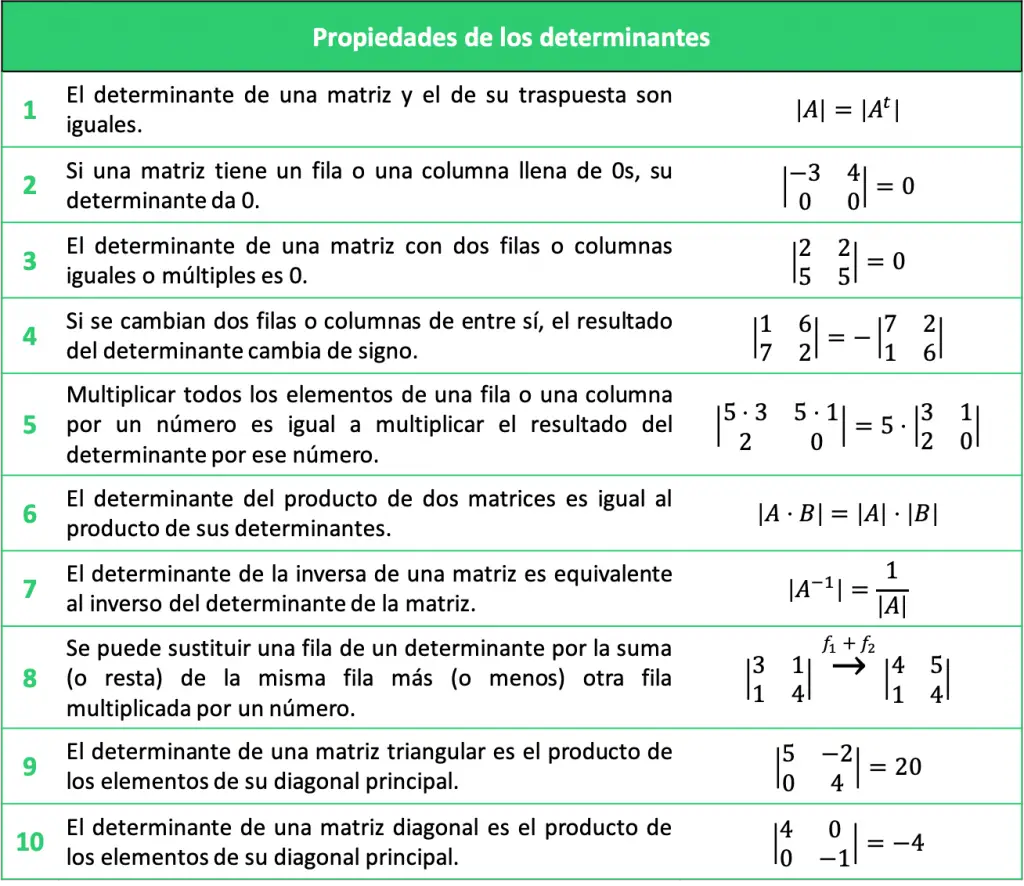
Ejercicios resueltos con propiedades de los determinantes

Ejercicio 1

Resuelve el siguiente determinante:

$\displaystyle \begin{vmatrix} 3 & 1 & 0 \\[1.1ex] 4 & 2 & 0 \\[1.1ex] -1 & 6 & 0 \end{vmatrix}$

Ver solución

Si un determinante tiene una fila o una columna llena de ceros, el determinante da 0 (propiedad 2). Por tanto, el resultado del determinante es 0, porque la tercera columna está llena de ceros.

Ejercicio 2

Resuelve el siguiente determinante:

$\displaystyle \begin{vmatrix} 4 & 2 & -3 & 5 \\[1.1ex] 1 & 5 & 3 & 2 \\[1.1ex]4 & 2 & -3 & 5 \\[1.1ex] -2 & 0 & 4 & 3 \end{vmatrix}$

Ver solución

Si un determinante tiene dos filas o dos columnas iguales o múltiples, el determinante da 0 (propiedad 3). Por lo tanto, el resultado del determinante es 0, porque la primera fila y la tercera fila son iguales.

Ejercicio 3

Calcula el siguiente determinante:

$\displaystyle \begin{vmatrix} 1 & 0 & 2 & 2 \\[1.1ex] 3 & 1 & 5 & 6 \\[1.1ex] 1 & 3 & -2 & 2 \\[1.1ex] 2 & 2 & 0 & 4 \end{vmatrix}$

Ver solución

Si un determinante tiene dos filas o dos columnas iguales o múltiples, el determinante da 0 (propiedad 3). Por lo tanto, el resultado del determinante es 0, porque la cuarta columna es el doble de la primera columna.

Ejercicio 4

Conocemos el resultado de un determinante, aunque no sabemos los elementos de la matriz:

$\displaystyle \begin{vmatrix} a & b \\[1.1ex] c & d \end{vmatrix} = 3$

A partir del resultado del determinante anterior y de las propiedades de los determinantes, calcula el resultado de los siguientes determinantes:

$\displaystyle \mathbf{a} \bm{)} \ \begin{vmatrix} a & c \\[1.1ex] b & d \end{vmatrix} \qquad \mathbf{b} \bm{)} \ \begin{vmatrix} b & a \\[1.1ex] d & c \end{vmatrix} \qquad \mathbf{c} \bm{)} \ \begin{vmatrix} a & 3b \\[1.1ex] c & 3d \end{vmatrix}$

Ver solución

a) $\begin{pmatrix} a & c \\ b & d \end{pmatrix}$ es la matriz traspuesta de $\begin{pmatrix} a & b \\ c & d \end{pmatrix}$ . Y el determinante de una matriz es igual al determinante de su matriz traspuesta (propiedad 1). Por tanto, el resultado de este determinante también es 3.

$\displaystyle \begin{vmatrix} a & c \\[1.1ex] b & d \end{vmatrix}=\begin{vmatrix} a & b \\[1.1ex] c & d \end{vmatrix}=\bm{3}$

b) En el determinante $\begin{vmatrix} b & a \\ d & c \end{vmatrix}$ se han cambiado las columnas 1 y 2 entre sí respecto al determinante del enunciado $\begin{vmatrix} a & b \\ c & d \end{vmatrix}$ . Por lo tanto, según la propiedad 4, el resultado es el mismo que el resultado del determinante del enunciado pero cambiado de signo, es decir, -3.

$\displaystyle \begin{vmatrix} b & a \\[1.1ex] d & c \end{vmatrix} = - \begin{vmatrix} a & b \\[1.1ex] c & d \end{vmatrix}= \bm{-3}$

c) En el determinante $\begin{vmatrix} a & 3b \\ c & 3d \end{vmatrix}$ se ha multiplicado toda la segunda columna del determinante del enunciado por 3. Por tanto, a partir de la propiedad 5, podemos deducir que su resultado también será el resultado del determinante del enunciado multiplicado por 3, es decir, 9.

$\displaystyle \begin{vmatrix} a & 3b \\[1.1ex] c & 3d \end{vmatrix} =3 \begin{vmatrix} a & b \\[1.1ex] c & d \end{vmatrix} =3 \cdot 3 = \bm{9}$

Ejercicio 5

Sabemos el resultado de estos dos determinantes:

$\displaystyle\vert A \vert = \begin{vmatrix} 1 & 2 & 0 & 1 \\[1.1ex] -2 & -1 & 1 & 0 \\[1.1ex] 1 & 3 & 3 & -1 \\[1.1ex] 3 & 4 & 1 & 1 \end{vmatrix}=8$

$\displaystyle\vert B \vert = \begin{vmatrix} 0 & 1 & 3 & 2 \\[1.1ex] -1 & -2 & 0 & 0 \\[1.1ex] 3 & 1 & 1 & 2 \\[1.1ex] -1 & 2 & 3 & 1 \end{vmatrix} = - 4$

A partir de esta información, calcula:

$\displaystyle \vert A \cdot B \vert$

Ver solución

Para calcular el resultado del determinante, no hace falta hacer la multiplicación de las matrices 4×4. Ya que el determinante del producto de dos matrices es igual al producto del determinante de cada matriz por separado (propiedad 6). Por tanto:

$\vert A \cdot B \vert = \vert A \vert \cdot \vert B \vert = 8 \cdot (-4) = \bm{-32}$

8 comentarios en “Propiedades de los determinantes”

Ana
26/08/2020 a las 12:05

Gracias

Responder
1. marc.gisbert@matricesydeterminantes.com
  28/08/2020 a las 11:39
  
  A ti;)
  
  Responder
Ignacio Galicia
11/11/2020 a las 01:23

Muy buena aportación, la mayoría, incluyendo libros solo manejan matrices y determinantes de 3X3

Responder
1. Matrices y Determinantes
  13/11/2020 a las 10:15
  
  ¡Muchas gracias Ignacio!
  
  Responder
Allen
27/01/2022 a las 04:27

¿En donde encuentro la demostración de la propiedad 6 ?

Responder
1. Matrices y Determinantes
  30/01/2022 a las 14:42
  
  Hola Allen,
  
  Te dejo la demostración de esta propiedad de los determinantes a continuación.
  
  Sean dos matrices cualesquiera:
  $\displaystyle A=\begin{pmatrix}a&b\\[1.1ex]c&d\end{pmatrix} \qquad B=\begin{pmatrix}e&f\\[1.1ex]g&h\end{pmatrix}$
  
  El determinante del producto de las dos matrices es:
  
  $\displaystyle\begin{pmatrix}a&b\\[1.1ex]c&d\end{pmatrix}\cdot \begin{pmatrix}e&f\\[1.1ex]g&h\end{pmatrix}=\begin{pmatrix}ae+bg&af+bh\\[1.1ex]ce+dg&cf+dh\end{pmatrix}$
  
  $\begin{aligned}\displaystyle\begin{vmatrix}ae+bg&af+bh\\[1.1ex]ce+dg&cf+dh\end{vmatrix} & =bcgf-afdg-ebch+eadh+bgdh-bhdg \\ & =bcgf-afdg-ebch+eadh\end{aligned}$
  
  Por otro lado, si primero calculamos el determinante de cada matriz por separado y luego multiplicamos el resultado obtenemos la siguiente expresión algebraica:
  
  $\displaystyle\begin{vmatrix}a&b\\[1.1ex]c&d\end{vmatrix}=ad-bc \qquad \begin{vmatrix}e&f\\[1.1ex]g&h\end{vmatrix}=eh-fg$
  
  $(ad-bc)\cdot (eh-fg)=adeh-adfg-bceh+bcfg$
  
  Como puedes ver, se consigue la misma expresión con las dos operaciones. En este caso se ha demostrado para determinantes 2×2, pero puedes aplicar el mismo procedimiento para demostrar la misma propiedad con determinantes de dimensiones más grandes.
  
  Responder
Todo
20/10/2022 a las 01:47

¿Comó es el determinante de una suma?

Responder
1. Matrices y Determinantes
  26/10/2022 a las 13:57
  
  Buenas,
  
  Para calcular el determinante de una suma de matrices primero debes sumar las matrices y luego calcular el determinante, no hay otra opción. A diferencia del producto matricial, si primero haces el determinante de cada matriz y luego sumas los resultados, el resultado final no es el mismo.
  
  Responder

Propiedad 1: Determinante de la matriz transpuesta

Ejemplo:

Propiedad 2: Determinante con una fila o columna llena de ceros

Ejemplo:

Propiedad 3: Determinante con dos filas o columnas iguales

Ejemplo:

Propiedad 4: Cambiar filas o columnas de un determinante

Ejemplo:

Propiedad 5: Multiplicar una línea de una determinante por un escalar

Ejemplo:

Propiedad 6: Determinante del producto matricial

Ejemplo:

Propiedad 7: Determinante de la matriz inversa

Ejemplo:

Propiedad 8: Sustituir la fila de un determinante

Ejemplo:

Propiedad 9: Determinante de una matriz triangular

Ejemplo:

Propiedad 10: Determinante de una matriz diagonal

Ejemplo:

Tabla resumen de las propiedades de los determinantes

Ejercicios resueltos con propiedades de los determinantes

Ejercicio 1

Ejercicio 2

Ejercicio 3

Ejercicio 4

Ejercicio 5

8 comentarios en “Propiedades de los determinantes”

Deja un comentario Cancelar respuesta