⭐ Determinantes ✅

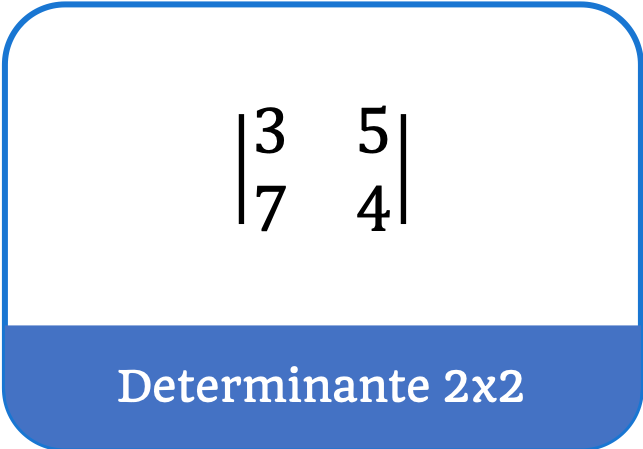
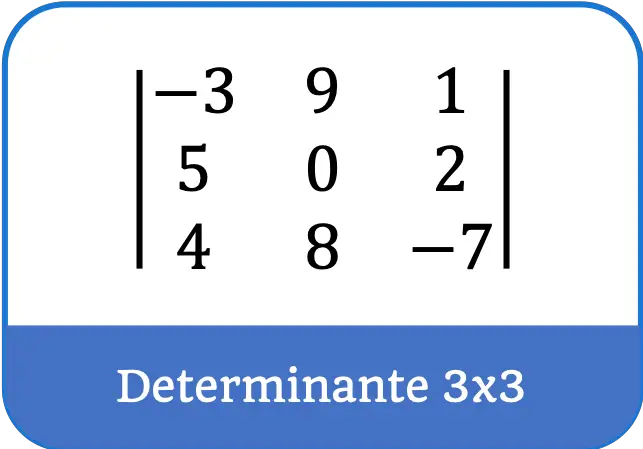
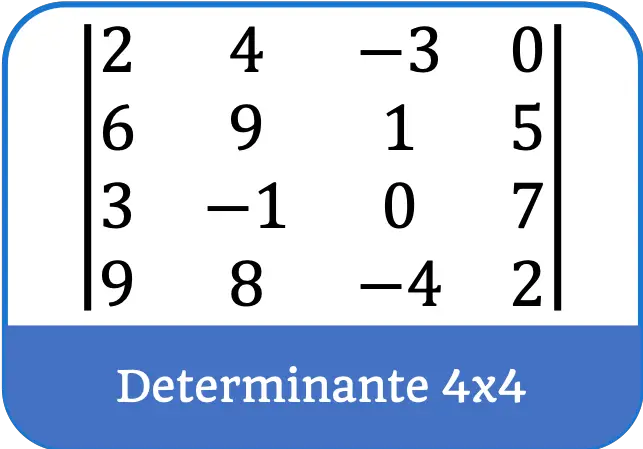
¿Qué es el determinante de una matriz?

Un determinante es una matriz cuadrada representada con una barra vertical a cada lado de la matriz.

Por ejemplo, si tenemos la siguiente matriz:

$\displaystyle A =\begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\[1.1ex] a_{21} & a_{22} & \cdots & a_{2n} \\[1.1ex] \vdots & \vdots & \ddots & \vdots \\[1.1ex] a_{n1} & a_{n2} & \cdots & a_{nn} \end{pmatrix}$

El determinante de la matriz A se representa de la siguiente manera:

$\displaystyle\begin{vmatrix} A \end{vmatrix} = \begin{vmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\[1.1ex] a_{21} & a_{22} & \cdots & a_{2n} \\[1.1ex] \vdots & \vdots & \ddots & \vdots \\[1.1ex] a_{n1} & a_{n2} & \cdots & a_{nn} \end{vmatrix} \right)$

Es importante tener en cuenta que solo se pueden resolver determinantes de matrices cuadradas.