Resolver un sistema de ecuaciones por el método de Gauss

En esta página aprenderás qué es el método de Gauss-Jordan y cómo resolver un sistema de ecuaciones por el método de Gauss. Además, también encontrarás ejemplos y ejercicios resueltos de sistemas con el método de Gauss para que puedas practicar y entenderlo a la perfección.

Sumario

1. ¿Qué es el método de Gauss?

2. Matriz ampliada al sistema

3. Transformaciones de filas permitidas

4. ¿Cómo resolver un sistema de ecuaciones por el método de Gauss?

5. Ejercicios resueltos de sistemas de ecuaciones por el método de Gauss-Jordan

¿Qué es el método de Gauss?

El método de Gauss-Jordan es un procedimiento que sirve para resolver sistemas de ecuaciones con 3 incógnitas, o sea como este:

$\left. \begin{array}{r} 3x-4y+5z=10 \\[2ex] x+5y-2z=4 \\[2ex] -x+4y+2z=-1 \end{array} \right\}$

El objetivo del método de Gauss es convertir el sistema de ecuaciones inicial en un sistema escalonado, es decir, un sistema en el cual cada ecuación tiene una incógnita menos que l’anterior:

$\left. \begin{array}{r} a_1x+b_1y+c_1z=d_1 \\[2ex] a_2x+b_2y+c_2z=d_2 \\[2ex] a_3x+b_3y+c_3z=d_3 \end{array} \right\} \ \bm{\longrightarrow} \left. \begin{array}{r} A_1x+B_1y+C_1z=D_1 \\[2ex] B_2y+C_2z=D_2 \\[2ex] C_3z=D_3 \end{array} \right\}$

Sin embargo, para llegar a hacer esto, primero debemos saber cómo expresar un sistema de ecuaciones en forma de matriz y las transformaciones permitidas en esta matriz. Así que explicaremos estas dos cosas antes, y luego veremos cómo utilizar el procedimiento del método de Gauss.

Matriz ampliada al sistema

Antes de ver cómo se resuelve el sistema, debemos saber que un sistema de ecuaciones se puede expresar en forma de matriz: los coeficientes de las $x}$ se ponen en la primera columna, los coeficientes de las $y}$ en la segunda columna, los coeficientes de las $z$ en la tercera columna y los números sin incógnita en la cuarta columna.

Por ejemplo:

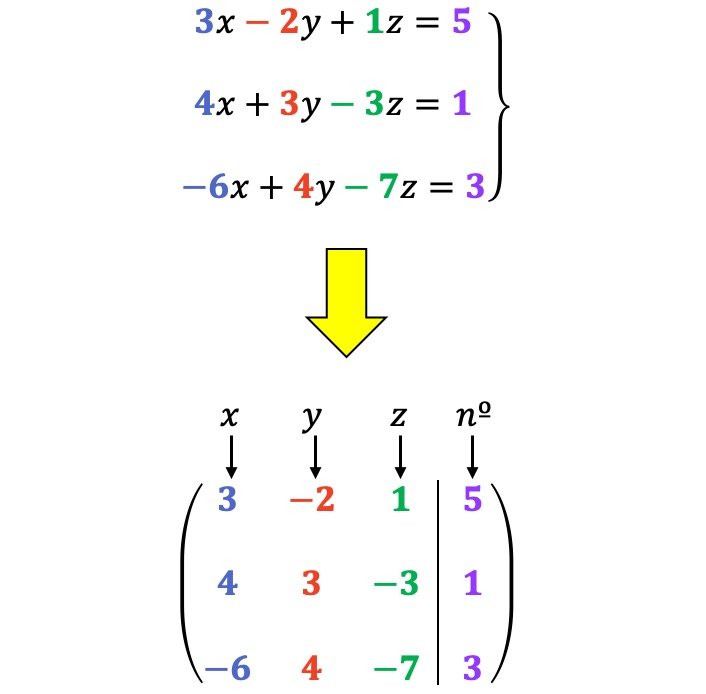
Transformaciones de filas permitidas

Para conseguir convertir el sistema de ecuaciones en un sistema escalonado, se puede hacer cualquier operación de las siguientes en la matriz asociada al sistema:

Cambiar el orden de las filas de la matriz.

Por ejemplo, podemos cambiar de orden las filas 2 y 3 de una matriz:

$\left( \begin{array}{ccc|c} 3 & 5 & -2 & 1 \\[2ex] -2 & 4 & -1 & 2 \\[2ex] 6 & 1 & -3 & 10 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{ f_2 \rightarrow f_3}} \\[2ex] \xrightarrow{ f_3 \rightarrow f_2}} \end{array} \left( \begin{array}{ccc|c} 3 & 5 & -2 & 1 \\[2ex] 6 & 1 & -3 & 10 \\[2ex] -2 & 4 & -1 & 2 \end{array} \right)$

Multiplicar o dividir todos los términos de una fila por un número diferente de 0.

Por ejemplo, podemos multiplicar la fila 1 por 4, y dividir la fila 3 entre 2:

$\left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] 3 & -1 & 5 & -3 \\[2ex] 2 & -4 & -2 & 6 \end{array} \right) \begin{array}{c} \xrightarrow{4 f_1} \\[2ex] \\[2ex] \xrightarrow{ f_3 / 2} \end{array} \left( \begin{array}{ccc|c} 4 & -8 & 12 & 4 \\[2ex] 3 & -1 & 5 & -3 \\[2ex] 1 & -2 & -1 & 3 \end{array} \right)$

Sustituir una fila por la suma de la misma fila más otra fila multiplicada por un número.

Por ejemplo, en la siguiente matriz sumamos a la fila 2 la fila 3 multiplicada por 1:

$\left( \begin{array}{ccc|c} -1 & -3 & 4 & 1 \\[2ex] 2 & 4 & 1 & -5 \\[2ex] 1 & -2 & 3 & -1 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 + 1 \cdot f_3} \\[2ex] & \end{array} \left( \begin{array}{ccc|c} -1 & -3 & 4 & 1 \\[2ex] 3 & 2 & 4 & -6 \\[2ex] 1 & -2 & 3 & -1 \end{array} \right)$

¿Cómo resolver un sistema de ecuaciones por el método de Gauss?

Ahora vamos a ver mediante un ejemplo el procedimiento de cómo resolver un sistema de ecuaciones con el método de Gauss:

$\left. \begin{array}{r} -x+2y+2z=-24 \\[2ex] x+y+z=48 \\[2ex] 2x-6y+4z=12 \end{array} \right\}$

Lo primero que tenemos que hacer es la matriz ampliada del sistema:

ejemplo de sistema de ecuaciones resuelto por el método de Gauss

Como veremos luego, es mejor si el primer número de la primera fila es un 1. Por tanto, vamos a cambiar de orden las filas 1 y 2:

$\left( \begin{array}{ccc|c} -1 & 2 & 2 &-24 \\[2ex] 1 & 1 & 1 & 48 \\[2ex] 2 & -6 & 4 & 12 \end{array} \right) \begin{array}{c} \xrightarrow{ f_1 \rightarrow f_2} \\[2ex] \xrightarrow{ f_2 \rightarrow f_1} \\[2ex] & \end{array} \left( \begin{array}{ccc|c} \color{blue}\boxed{\color{black}1} & 1 & 1 & 48 \\[2ex] -1 & 2 & 2 &-24 \\[2ex] 2 & -6 & 4 & 12 \end{array} \right)$

El objetivo del método de Gauss es conseguir que los números por debajo de la diagonal principal sean 0. Es decir, tenemos que convertir los números de color rojo en 0:

$\left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] \color{red}\bm{-1} & 2 & 2 &-24 \\[2ex] \color{red}\bm{2} & \color{red}\bm{-6} & 4 & 12 \end{array} \right)$

Para eliminar estos números debemos hacer las transformaciones adecuadas de las filas.

Por ejemplo, el -1, que es el primer elemento de la segunda fila, es el negativo de 1, el primer elemento de la primera fila. Por tanto, si a la segunda fila le sumamos la primera fila, se eliminará el -1:

$\begin{array}{lccc|c} & -1 & 2 & 2 & -24 \\ + & \phantom{-}1 & 1 & 1 & \phantom{-}48 \\ \hline & \phantom{-}0 & 3 & 3 & \phantom{-}24 \end{array} \begin{array}{l} \color{blue}\bm{\leftarrow f_2} \\ \color{blue}\bm{\leftarrow f_1} \\ \phantom{hline} \\ \end{array}$

Así que si hacemos esta suma nos queda la siguiente matriz:

$\left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] -1 & 2 & 2 & -24 \\[2ex] 2 & -6 & 4 & 12 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 + f_1} \\[2ex] & \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] \color{blue}\boxed{\color{black}0} & 3 & 3 & 24 \\[2ex] 2 & -6 & 4 & 12 \end{array} \right)$

De esta manera hemos conseguido transformar el -1 en un 0.

Ahora vamos a transformar el 2. Si te fijas, el 2, que es el primer elemento de la tercera fila, es el doble de 1, el primer elemento de la primera fila. Por tanto, si a la tercera fila le sumamos la primera fila multiplicada por -2, se eliminará el 2:

$\begin{array}{lccc|c} & \phantom{-}2 & -6 & \phantom{-}4 & \phantom{-}12 \\ + & -2 & -2 & -2 & -96 \\ \hline & \phantom{-}0 & -8 & \phantom{-}2 & -84 \end{array} \begin{array}{l} \color{blue} \bm{\leftarrow f_3} \\ \color{blue} \bm{\leftarrow -2 f_1} \\ \phantom{hline} \\ \end{array}$

Así que nos queda la siguiente matriz:

$\left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] 0 & 3 & 3 & 24 \\[2ex] 2 & -6 & 4 & 12 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3-2f_1} \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] 0 & 3 & 3 & 24 \\[2ex] \color{blue}\boxed{\color{black}0} & -8 & 2 & -84 \end{array} \right)$

De esta manera hemos conseguido transformar el 2 en un 0.

Ahora solo nos queda convertir el -8 en 0. Para ello, multiplicamos la tercera fila por 3 y le sumamos la segunda fila multiplicada por 8:

$\begin{array}{lccc|r} & 0 & -24 & \phantom{2}6 & -252 \\ + & 0 & \phantom{-}24 & 24 & \phantom{-}192 \\ \hline & 0 & \phantom{-2}0 & 30 & -60 \end{array} \begin{array}{l}\color{blue}\bm{ \leftarrow 3f_3} \\\color{blue}\bm{ \leftarrow 8f_2} \\ \phantom{hline} \\ \end{array}$

Por tanto, obtenemos la siguiente matriz:

$\left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] 0 & 3 & 3 & 24 \\[2ex] 0 & -8 & 2 & -84 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{3f_3 + 8f_2} \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] 0 & 3 & 3 & 24 \\[2ex] 0 & \color{blue}\boxed{\color{black}0} & 30 & -60 \end{array} \right)$

Y con estas transformaciones hemos conseguido que todos los números por debajo de la diagonal principal sean 0. Así que ya podemos resolver el sistema de ecuaciones.

Ahora debemos convertir la matriz en un sistema de ecuaciones con incógnitas. Para ello recuerda que la primera columna corresponde a la $x$ , la segunda columna a la $y$ , la tercera columna a la $z$ y la última columna son los números sin incógnitas:

$\left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] 0 & 3 & 3 & 24 \\[2ex] 0 & 0 & 30 & -60 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} 1x+1y+1z=48 \\[2ex] 3y+3z=24 \\[2ex] 30z=-60 \end{array} \right\}$

Y, finalmente, para resolver el sistema tenemos que ir despejando las incógnitas de las ecuaciones de abajo hacia arriba. Ya que la última ecuación solo tiene una incógnita, y, por tanto, la podemos despejar y encontrar su valor:

$30z=-60$

$z = \cfrac{-60}{30}$

$\bm{z=-2}$

Ahora que sabemos cuánto es z, si sustituimos su valor en la segunda ecuación podemos encontrar el valor de $y$ :

$3y+3z=24 \ \xrightarrow{z \ = \ -2} \ 3y+3(-2)=24$

$3y-6=24$

$3y=24+6$

$3y=30$

$y=\cfrac{30}{3}$

$\bm{y=10}$

Y hacemos lo mismo con la primera ecuación: sustituimos los valores de las otras incógnitas y despejamos $x$ :

$1x+1y+1z=48 \ \xrightarrow{y \ = \ 10 \ ; \ z \ = \ -2} \ 1x+1(10)+1(-2)=48$

$x+10-2=48$

$x=48-10+2$

$\bm{x=40}$

Por tanto la solución al sistema de ecuaciones es:

$\bm{x=40} \quad \bm{y=10} \quad \bm{z=-2}$

Ejercicios resueltos de sistemas de ecuaciones por el método de Gauss-Jordan

Ejercicio 1

Resuelve el siguiente sistema de ecuaciones con el método de Gauss:

$\left. \begin{array}{r} x+y-z=2 \\[2ex] x-2y+3z=0 \\[2ex] 2x-y+3z=3 \end{array} \right\}$

Ver solución

Lo primero que tenemos que hacer es la matriz ampliada del sistema:

$\left. \begin{array}{r} x+y-z=2 \\[2ex] x-2y+3z=0 \\[2ex] 2x-y+3z=3 \end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 1 & 1 & -1 & 2 \\[2ex] 1 & -2 & 3 & 0 \\[2ex] 2 & -1 & 3 & 3 \end{array} \right)$

Ahora debemos conseguir que todos los números por debajo de la matriz principal sean 0.

Así que hacemos operaciones con las filas para anular los dos últimos términos de la primera columna:

$\left( \begin{array}{ccc|c}1 & 1 & -1 & 2 \\[2ex] 1 & -2 & 3 & 0 \\[2ex] 2 & -1 & 3 & 3 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 -f_1} \\[2ex] \xrightarrow{f_3-2f_1} & \end{array} \left( \begin{array}{ccc|c} 1 & 1 & -1 & 2 \\[2ex] 0 & -3 & 4 & -2 \\[2ex] 0 & -3 & 5 & -1 \end{array} \right)$

Ahora eliminamos el último elemento de la segunda columna:

$\left( \begin{array}{ccc|c}1 & 1 & -1 & 2 \\[2ex] 0 & -3 & 4 & -2 \\[2ex] 0 & -3 & 5 & -1 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3-f_2} & \end{array} \left( \begin{array}{ccc|c} 1 & 1 & -1 & 2 \\[2ex] 0 & -3 & 4 & -2 \\[2ex] 0 & 0 & 1 & 1 \end{array} \right)$

Una vez todos los números por debajo de la diagonal principal son 0, ya podemos resolver el sistema de ecuaciones. Para ello volvemos a expresar la matriz en forma de sistema de ecuaciones con incógnitas:

$\left( \begin{array}{ccc|c} 1 & 1 & -1 & 2 \\[2ex] 0 & -3 & 4 & -2 \\[2ex] 0 & 0 & 1 & 1 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} x+y-z=2 \\[2ex] -3y+4z=-2 \\[2ex] 1z=1 \end{array} \right\}$

Y despejamos las incógnitas de las ecuaciones de abajo hacia arriba. Primero resolvemos la última ecuación:

$1z= 1$

$z=\bm{1}$

Ahora sustituimos el valor de z en la segunda ecuación para encontrar el valor de y:

$-3y+4z=-2 \ \xrightarrow{z \ = \ 1} \ -3y+4(1)=-2$

$-3y+4=-2$

$-3y=-2-4$

$-3y=-6$

$y=\cfrac{-6}{-3} = \bm{2}$

Y hacemos lo mismo con la primera ecuación: sustituimos los valores de las otras incógnitas y despejamos x:

$x+y-z=2 \ \xrightarrow{y \ = \ 2 \ ; \ z \ = \ 1} \ x+(2)-(1)=2$

$x+1=2$

$x=2-1$

$\bm{x=1}$

Por tanto, la solución del sistema de ecuaciones es:

$\bm{x=1} \qquad \bm{y=2} \qquad \bm{z=1}$

Ejercicio 2

Halla la solución del siguiente sistema de ecuaciones por el método de Gauss:

$\left. \begin{array}{r} 2x+y+2z=-3 \\[2ex] x+3y+2z=5 \\[2ex] 4x+2y-z=-1 \end{array} \right\}$

Ver solución

Lo primero que tenemos que hacer es la matriz ampliada del sistema:

$\left. \begin{array}{r} 2x+y+2z=-3 \\[2ex] x+3y+2z=5 \\[2ex] 4x+2y-z=-1 \end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 2 & 1 & 2 & -3 \\[2ex] 1 & 3 & 2 & 5 \\[2ex] 4 & 2 & -1 & -1 \end{array} \right)$

Para aplicar el método de Gauss, es más fácil si el primer número de la primera fila es un 1. Por tanto, cambiaremos de orden las filas 1 y 2:

$\left( \begin{array}{ccc|c}2 & 1 & 2 & -3 \\[2ex] 1 & 3 & 2 & 5 \\[2ex] 4 & 2 & -1 & -1 \end{array} \right) \begin{array}{c} \xrightarrow{f_1\rightarrow f_2} \\[2ex] \xrightarrow{f_2\rightarrow f_1} \\[2ex] & \end{array} \left( \begin{array}{ccc|c}1 & 3 & 2 & 5 \\[2ex] 2 & 1 & 2 & -3 \\[2ex] 4 & 2 & -1 & -1\end{array} \right)$

Ahora debemos conseguir que todos los números por debajo de la matriz principal sean 0.

De modo que realizamos operaciones con las filas para anular los dos últimos elementos de la primera columna:

$\left( \begin{array}{ccc|c} 1 & 3 & 2 & 5 \\[2ex] 2 & 1 & 2 & -3 \\[2ex] 4 & 2 & -1 & -1 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 -2f_1} \\[2ex] \xrightarrow{f_3-4f_1} & \end{array} \left( \begin{array}{ccc|c} 1 & 3 & 2 & 5 \\[2ex] 0 & -5 & -2 & -13 \\[2ex] 0 & -10 & -9 & -21 \end{array} \right)$

Ahora convertimos en cero el último elemento de la segunda columna:

$\left( \begin{array}{ccc|c}1 & 3 & 2 & 5 \\[2ex] 0 & -5 & -2 & -13 \\[2ex] 0 & -10 & -9 & -21\end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3-2f_2} & \end{array} \left( \begin{array}{ccc|c} 1 & 3 & 2 & 5 \\[2ex] 0 & -5 & -2 & -13 \\[2ex] 0 & 0 & -5 & 5 \end{array} \right)$

Una vez todos los números por debajo de la diagonal principal son 0, ya podemos solucionar el sistema de ecuaciones. Para ello volvemos a expresar la matriz en forma de sistema de ecuaciones con incógnitas:

$\left( \begin{array}{ccc|c} 1 & 3 & 2 & 5 \\[2ex] 0 & -5 & -2 & -13 \\[2ex] 0 & 0 & -5 & 5 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} x+3y+2z=5 \\[2ex] -5y-2z=-13 \\[2ex] -5z=5 \end{array} \right\}$

Y despejamos las incógnitas de las ecuaciones de abajo hacia arriba. Primero resolvemos la última ecuación:

$-5z= 5$

$z=\cfrac{5}{-5}=\bm{-1}$

Ahora sustituimos el valor de z en la segunda ecuación para encontrar el valor de y:

$-5y-2z=-13 \ \xrightarrow{z \ = \ -1} \ -5y-2(-1)=-13$

$-5y+2=-13$

$-5y=-13-2$

$-5y=-15$

$y=\cfrac{-15}{-5} = \bm{3}$

Y hacemos lo mismo con la primera ecuación: sustituimos los valores de las otras incógnitas y despejamos x:

$x+3y+2z=5 \ \xrightarrow{y \ = \ 3 \ ; \ z \ = \ -1} \ x+3(3)+2(-1)=5$

$x+9-2=5$

$x=5-9+2$

$\bm{x=-2}$

Por tanto, la solución del sistema de ecuaciones es:

$\bm{x=-2} \qquad \bm{y=3} \qquad \bm{z=-1}$

Ejercicio 3

Calcula la solución del siguiente sistema de ecuaciones por el método de Gauss:

$\left. \begin{array}{r} 2x+3y+z=-1 \\[2ex] 6x+4y+4z=0 \\[2ex] -4x+2y-z=5 \end{array} \right\}$

Ver solución

Lo primero que tenemos que hacer es la matriz ampliada del sistema:

$\left. \begin{array}{r} 2x+3y+z=-1 \\[2ex] 6x+4y+4z=0 \\[2ex] -4x+2y-z=5\end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 2 & 3 & 1 & -1 \\[2ex] 6 & 4 & 4 & 0 \\[2ex] -4 & 2 & -1 & 5 \end{array} \right)$

Ahora debemos lograr que todos los números por debajo de la matriz principal sean 0.

De manera que realizamos operaciones con las filas para anular los dos últimos elementos de la primera columna:

$\left( \begin{array}{ccc|c} 2 & 3 & 1 & -1 \\[2ex] 6 & 4 & 4 & 0 \\[2ex] -4 & 2 & -1 & 5\end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 -3f_1} \\[2ex] \xrightarrow{f_3+2f_1} & \end{array} \left( \begin{array}{ccc|c} 2 & 3 & 1 & -1 \\[2ex] 0 & -5 & 1 & 3 \\[2ex] 0 & 8 & 1 & 3\end{array} \right)$

Ahora convertimos en cero el último elemento de la segunda columna:

$\left( \begin{array}{ccc|c}2 & 3 & 1 & -1 \\[2ex] 0 & -5 & 1 & 3 \\[2ex] 0 & 8 & 1 & 3\end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{5f_3+8f_2} & \end{array} \left( \begin{array}{ccc|c} 2 & 3 & 1 & -1 \\[2ex] 0 & -5 & 1 & 3 \\[2ex] 0 & 0 & 13 & 39 \end{array} \right)$

$\left( \begin{array}{ccc|c} 2 & 3 & 1 & -1 \\[2ex] 0 & -5 & 1 & 3 \\[2ex] 0 & 0 & 13 & 39\end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} 2x+3y+1z=-1 \\[2ex] -5y+z=3 \\[2ex] 13z=39 \end{array} \right\}$

Y despejamos las incógnitas de las ecuaciones de abajo hacia arriba. Primero resolvemos la última ecuación:

$13z= 39$

$z=\cfrac{39}{13}=\bm{3}$

Ahora sustituimos el valor de z en la segunda ecuación para encontrar el valor de y:

$-5y+z=3 \ \xrightarrow{z \ = \ 3} \ -5y+(3)=3$

$-5y=3-3$

$-5y=0$

$y=\cfrac{0}{-5} = \bm{0}$

Y hacemos lo mismo con la primera ecuación: sustituimos los valores de las otras incógnitas y despejamos x:

$2x+3y+1z=-1 \ \xrightarrow{y \ = \ 0 \ ; \ z \ = \ 3} \ 2x+3(0)+1(3)=-1$

$2x+0+3=-1$

$2x=-1-3$

$2x=-4$

$x=\cfrac{-4}{2}=\bm{-2}$

Por lo tanto, la solución del sistema de ecuaciones es:

$\bm{x=-2} \qquad \bm{y=0} \qquad \bm{z=3}$

Ejercicio 4

Soluciona el siguiente sistema de ecuaciones con 3 incógnitas por el método de Gauss:

$\left. \begin{array}{r} 2x-6=4y+6z \\[2ex] -y-3z=1-3x \\[2ex] -4x-y=6-3z \end{array} \right\}$

Ver solución

Antes de aplicar el método de Gauss, debemos ordenar el sistema de ecuaciones para que todas las incógnitas estén en el lado izquierdo de la ecuación y los números en el derecho:

$\left. \begin{array}{r}2x-6=4y+6z \\[2ex] -y-3z=1-3x \\[2ex] -4x-y=6-3z \end{array} \right\} \longrightarrow \left. \begin{array}{r} 2x-4y-6z=6 \\[2ex] 3x-y-3z=1 \\[2ex] -4x-y+3z=6\end{array} \right\}$

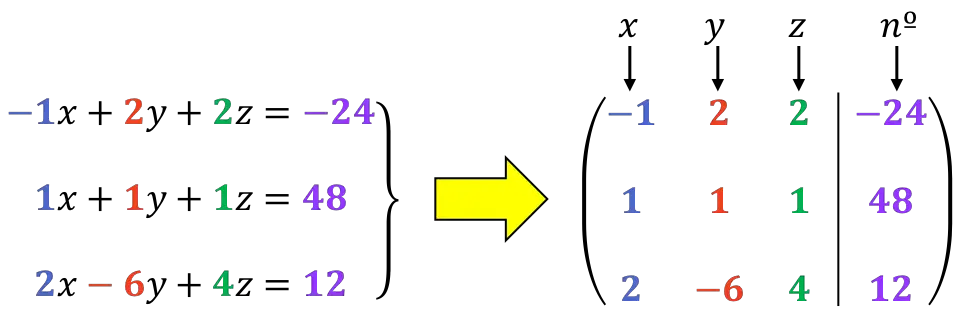
Una vez el sistema está ordenado, construimos la matriz ampliada del sistema:

$\left. \begin{array}{r} 2x-4y-6z=6 \\[2ex] 3x-y-3z=1 \\[2ex] -4x-y+3z=6 \end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 2 & -4 & -6 & 6 \\[2ex] 3 & -1 & -3 & 1 \\[2ex] -4 & -1 & 3 & 6 \end{array} \right)$

Como todos los números de la primera fila son pares, antes de operar con las filas dividiremos la primera fila entre 2. Ya que esto nos facilitará los cálculos:

$\left( \begin{array}{ccc|c}2 & -4 & -6 & 6 \\[2ex] 3 & -1 & -3 & 1 \\[2ex] -4 & -1 & 3 & 6 \end{array} \right) \begin{array}{c} \xrightarrow{f_1/2} \\[2ex] \\[2ex] & \end{array} \left( \begin{array}{ccc|c}1 & -2 & -3 & 3 \\[2ex] 3 & -1 & -3 & 1 \\[2ex] -4 & -1 & 3 & 6\end{array} \right)$

Ahora debemos conseguir que todos los números por debajo de la matriz principal sean 0.

De modo que realizamos operaciones con las filas para anular los dos últimos elementos de la primera columna:

$\left( \begin{array}{ccc|c} 1 & -2 & -3 & 3 \\[2ex] 3 & -1 & -3 & 1 \\[2ex] -4 & -1 & 3 & 6 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 -3f_1} \\[2ex] \xrightarrow{f_3+4f_1} & \end{array} \left( \begin{array}{ccc|c} 1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & -9 & -9 & 18\end{array} \right)$

Igual que antes, como todos los números de la última fila son múltiples de 9, la dividiremos entre 9 para hacer los cálculos más fáciles:

$\left( \begin{array}{ccc|c}1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & -9 & -9 & 18 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex]\xrightarrow{f_3/9} & \end{array} \left( \begin{array}{ccc|c}1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & -1 & -1 & 2\end{array} \right)$

Ahora convertimos en cero el último elemento de la segunda columna:

$\left( \begin{array}{ccc|c}1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & -1 & -1 & 2\end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{5f_3+f_2} & \end{array} \left( \begin{array}{ccc|c} 1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & 0 & 1 & 2 \end{array} \right)$

$\left( \begin{array}{ccc|c} 1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & 0 & 1 & 2 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} x-2y-3z=3 \\[2ex] 5y+6z=-8 \\[2ex] 1z=2 \end{array} \right\}$

Y despejamos las incógnitas de las ecuaciones de abajo hacia arriba. Primero resolvemos la última ecuación:

$1z= 2$

$z=\bm{2}$

Ahora sustituimos el valor de z en la segunda ecuación para encontrar el valor de y:

$5y+6z=-8 \ \xrightarrow{z \ = \ 2} \ 5y+6(2)=-8$

$5y+12=-8$

$5y=-8-12$

$5y=-20$

$y=\cfrac{-20}{5} = \bm{-4}$

Y hacemos lo mismo con la primera ecuación: sustituimos los valores de las otras incógnitas y despejamos x:

$x-2y-3z=3 \ \xrightarrow{y \ = \ -4 \ ; \ z \ = \ 2} \ x-2(-4)-3(2)=3$

$x+8-6=3$

$x=3-8+6$

$\bm{x=1}$

Por tanto, la solución del sistema de ecuaciones es:

$\bm{x=-1} \qquad \bm{y=-4} \qquad \bm{z=2}$

8 comentarios en “Método de Gauss – Jordan”

Dolors Herbera
26/05/2020 a las 06:15

Estaria bién que contaras porqué funciona este método: No es difícil ver que al hacer cada una de las transformaciones que dices el sistema que obtienes tiene las mismas soluciones que el sitema original!!

Nota que poner el sistema en notación matricial, como lo cuentas tu, no es imprescindible, lo que resulta és más cómodo a la hora de operar. Si quieres realmente aprovechar la potencia del cálculo matricial, puedes observar que las operaciones por filas en la matriz ampliada corresponden a multiplicarla por una matriz invertible a la izquierda o, equivalentemente, multiplicar el sistema AX=B por una matriz invertible por la izquierda (de paso ves que el nuevo sistema tiene exactamente las mismas soluciones que el original)

Responder
1. marc.gisbert@matricesydeterminantes.com
  26/05/2020 a las 08:51
  
  Bienvenida Dolors y muchas gracias por tu aportación, estamos de acuerdo con lo que explicas. Evidentemente poner en forma matricial el sistema es tan solo para ayudar a resolver el sistema de ecuaciones, aunque, como bien dices, hay gente que prefiere resolverlo directamente sobre las ecuaciones sin transformar el sistema en una matriz. Lo explicamos de esta manera porque pensamos que es la mejor para resolver un sistema mediante el método de Gauss.
  
  Por otro lado, es verdad que a veces puede resultar más fácil y rápido calcular la solución del sistema de ecuaciones mediante la matriz inversa, pero para ello es necesario conocer algunos conceptos un poco más avanzados. Por eso tenemos otra página en la web donde hemos explicado detalladamente paso a paso cómo resolver un sistema de ecuaciones con la matriz inversa.
  
  Responder
José
11/02/2021 a las 02:14

Hola soy José, vuestra pagina y para mi nivel de estudio, me resulta de maravilla, todo esta muy claro de entender y pude aprender a resolver todos loa ejercicios. Salvo el Ejercicio 3, donde el valor hallado de las incógnitas No verifica con el de las ecuaciones. En vuestro desarrollo hay un paso que no le encuentro justificación, si pueden revisen ejercicio 3.
2 3 1 -1 2 3 1 -1
0 -5 1 3 0 -8 1 3 esta fila transformada no se como sale
0 8 1 3 (5.F8 + 8.F2) 0 0 13 39
No entiendo la fila 2 con 0 -5 1 3 por que se cambio 0 – 8 1 3
Gracias por su trabajo me resulta de mucha ayuda y espero puedan responder

Responder
1. Matrices y Determinantes
  11/02/2021 a las 18:45
  
  ¡Muchas gracias por tu apoyo José!
  Tienes razón el -5 se transformaba a -8 sin sentido ya que no se hacía ninguna operación en esa fila.
  Se trataba de un error, ya lo hemos corregido.👍
  De todos modos, este error no afectaba a la solución del ejercicio, por lo que la solución ya estaba bien.
  Si sigues teniendo alguna duda del ejercicio te la resolveremos con mucho gusto.
  
  Responder
Olga diaz
05/10/2021 a las 17:18

Muchas gracias. Buen resumen.

Responder
1. Matrices y Determinantes
  11/10/2021 a las 13:24
  
  ¡Muchas gracias por tu comentario Olga!
  
  Responder
Donnovan Rosales
28/10/2021 a las 23:41

Una maravillosa recopilación de información y excelente explicación, lo hacen muy sencillo para poder entenderlo
Se los gradezco

Responder
1. Matrices y Determinantes
  29/10/2021 a las 12:53
  
  ¡Muchas gracias Donnovan! ¡Intentamos hacerlo lo mejor que podemos!
  
  Responder

¿Qué es el método de Gauss?

Matriz ampliada al sistema

Transformaciones de filas permitidas

¿Cómo resolver un sistema de ecuaciones por el método de Gauss?

Ejercicios resueltos de sistemas de ecuaciones por el método de Gauss-Jordan

Ejercicio 1

Ejercicio 2

Ejercicio 3

Ejercicio 4

8 comentarios en “Método de Gauss – Jordan”

Deja un comentario Cancelar respuesta