▷ Teorema de Rouché-Frobenius (ejemplos y ejercicios resueltos)

En esta página descubriremos qué es el teorema de Rouché Frobenius y cómo calcular el rango de una matriz con él. También encontrarás ejemplos y ejercicios resueltos paso a paso con el teorema de Rouché-Frobenius.

Sumario

1. ¿Qué es el teorema de Rouché – Frobenius?

2. Enunciado del teorema de Rouché-Frobenius

3. Ejemplo de Sistema Compatible Determinado (SCD)

4. Ejemplo de Sistema Compatible Indeterminado (SCI)

5. Ejemplo de Sistema Incompatible (SI)

6. Ejercicios resueltos del teorema de Rouché – Frobenius

¿Qué es el teorema de Rouché – Frobenius?

El teorema de Rouché-Frobenius es un método que nos permite clasificar los sistemas de ecuaciones lineales. Es decir, el teorema de Rouché-Frobenius sirve para saber cuántas soluciones tiene un sistema de ecuaciones sin necesidad de resolverlo.

Hay 3 tipos de sistemas de ecuaciones:

Sistema Compatible Determinado (SCD): el sistema tiene una única solución.
Sistema Compatible Indeterminado (SCI): el sistema tiene infinitas soluciones.
Sistema Incompatible (SI): el sistema no tiene solución.

Además, el teorema de Rouché-Frobenius también nos permitirá más adelante hacer la resolución de sistemas por la regla de Cramer.

Enunciado del teorema de Rouché-Frobenius

El teorema de Rouché-Frobenius dice que $\displaystyle \bm{A}$ es la matriz formada por los coeficientes de las incógnitas de un sistema de ecuaciones. Y la matriz $\displaystyle \bm{A'}$ , o matriz ampliada, es la matriz formada por los coeficientes de las incógnitas de un sistema de ecuaciones y los términos independientes:

El teorema de Rouché-Frobenius nos permite saber de qué tipo de sistema de ecuaciones se trata según el rango de las matrices A y A’:

Si rango(A) = rango(A’) = número de incógnitas ⟶ Sistema Compatible Determinado (SCD)
Si rango(A) = rango(A’) < número de incógnitas ⟶ Sistema Compatible Indeterminado (SCI)
Si rango(A) $\bm{\neq}$ rango(A’) ⟶ Sistema Incompatible (SI)

Una vez ya sabemos qué dice el teorema de Rouché-Frobenius, vamos a ver cómo resolver ejercicios del teorema de Rouché-Frobenius. Así que a continuación tienes 3 ejemplos: un ejercicio resuelto mediante el teorema de cada tipo de sistema de ecuaciones.

Ejemplo de Sistema Compatible Determinado (SCD)

$\begin{cases} 2x+y-3z=0 \\[1.5ex] x+2y-z= 1 \\[1.5ex] 4x-2y+z = 3\end{cases}$

La matriz A y la matriz ampliada A’ del sistema son:

$\displaystyle A= \left( \begin{array}{ccc} 2 & 1 & -3 \\[1.1ex] 1 & 2 & -1 \\[1.1ex] 4 & -2 & 1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & -3 & 0 \\[1.1ex] 1 & 2 & -1 & 1 \\[1.1ex] 4 & -2 & 1 & 3\end{array} \right)$

Ahora calculamos el rango de la matriz A. Para ello, miramos si el determinante de toda la matriz es diferente de 0:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & -3 \\[1.1ex] 1 & 2 & -1 \\[1.1ex] 4 & -2 & 1 \end{vmatrix} = 25 \neq 0$

Como la matriz tiene un determinante 3×3 distinto de 0, la matriz A es de rango 3:

$\displaystyle rg(A)=3$

Una vez sabemos el rango de A, calculamos el rango de A’, que será como mínimo de rango 3 porque acabamos de ver que dentro tiene un determinante de orden 3 diferente de 0. A parte, no puede ser de rango 4, ya que no podemos hacer ningún determinante de orden 4. Por tanto, la matriz A’ también es de rango 3:

$\displaystyle rg(A')=3$

De manera que, como el rango de la matriz A es igual al rango de la matriz A’ y al número de incógnitas del sistema (3), sabemos por el teorema de Rouché Frobenius que se trata de un Sistema Compatible Determinado (SCD):

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 3 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}$

Ejemplo de Sistema Compatible Indeterminado (SCI)

$\begin{cases} x-y+2z=1 \\[1.5ex] 3x+2y+z= 5 \\[1.5ex] 2x+3y-z = 4\end{cases}$

La matriz A y la matriz ampliada A’ del sistema son:

$\displaystyle A= \left( \begin{array}{ccc} 1 & -1 & 2 \\[1.1ex] 3 & 2 & 1 \\[1.1ex] 2 & 3 & -1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & -1 & 2 & 1 \\[1.1ex] 3 & 2 & 1 & 5 \\[1.1ex] 2 & 3 & -1 & 4 \end{array} \right)$

Ahora calculamos el rango de la matriz A. Para ello, miramos si el determinante de toda la matriz es diferente de 0:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & -1 & 2 \\[1.1ex] 3 & 2 & 1 \\[1.1ex] 2 & 3 & -1 \end{vmatrix} = 0$

El determinante de toda la matriz A da 0, por lo que no es de rango 3. Para ver si es de rango 2, tenemos que encontrar una submatriz dentro de A cuyo determinante sea distinto de 0. Por ejemplo el de la esquina superior izquierda:

$\displaystyle \begin{vmatrix} 1 & -1 \\[1.1ex] 3 & 2 \end{vmatrix} = 5 \neq 0$

Como la matriz tiene un determinante de 2×2 distinto de 0, la matriz A es de rango 2:

$\displaystyle rg(A)=2$

Una vez sabemos el rango de A, calculamos el rango de A’. El determinante de las 3 primeras columnas ya sabemos que da 0, así que probamos con los otros determinantes 3×3 posibles:

$\displaystyle \begin{vmatrix}1 & -1 & 1 \\[1.1ex] 3 & 2 & 5 \\[1.1ex] 2 & 3 & 4\end{vmatrix} = 0 \quad \begin{vmatrix}1 & 2 & 1 \\[1.1ex] 3 & 1 & 5 \\[1.1ex] 2 & -1 & 4\end{vmatrix} = 0 \quad \begin{vmatrix} -1 & 2 & 1 \\[1.1ex] 2 & 1 & 5 \\[1.1ex] 3 & -1 & 4\end{vmatrix} = 0$

Todos los determinantes 3×3 de la matriz A’ son 0, por tanto, la matriz A’ tampoco será de rango 3. Sin embargo, dentro sí que tiene determinantes de orden 2 diferentes de 0. Por ejemplo:

$\displaystyle \begin{vmatrix} 1 & -1 \\[1.1ex] 3 & 2 \end{vmatrix} = 5 \neq 0$

Así que la matriz A’ será de rango 2:

$\displaystyle rg(A')=2$

El rango de la matriz A es igual al rango de la matriz A’ pero estos son más pequeños que el número de incógnitas del sistema (3). Por lo tanto, según el teorema de Rouché-Frobenius se trata de un Sistema Compatible Indeterminado (SCI):

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = 2 \ < \ n =3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCI}\phantom{^9_9}} \end{array}$

Ejemplo de Sistema Incompatible (SI)

$\begin{cases} 2x+y-2z=3 \\[1.5ex] 3x-2y+z= 2 \\[1.5ex] x+4-5z = 3 \end{cases}$

La matriz A y la matriz ampliada A’ del sistema son:

$\displaystyle A= \left( \begin{array}{ccc} 2 & 1 & -2 \\[1.1ex] 3 & -2 & 1 \\[1.1ex] 1 & 4 & -5 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & -2 & 3 \\[1.1ex] 3 & -2 & 1 & 2 \\[1.1ex] 1 & 4 & -5 & 3 \end{array} \right)$

Ahora calculamos el rango de la matriz A. Para ello, miramos si el determinante de toda la matriz es diferente de 0:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & -2 \\[1.1ex] 3 & -2 & 1 \\[1.1ex] 1 & 4 & -5 \end{vmatrix} = 0$

$\displaystyle \begin{vmatrix} 2 & 1 \\[1.1ex] 3 & -2 \end{vmatrix} = -7 \neq 0$

Como la matriz tiene un determinante de orden 2 distinto de 0, la matriz A es de rango 2:

$\displaystyle rg(A)=2$

Una vez sabemos el rango de A, calculamos el rango de A’. El determinante de las 3 primeras columnas ya sabemos que da 0, así que ahora probamos, por ejemplo, con el determinante de las 3 últimas columnas:

$\displaystyle \begin{vmatrix} 1 & -2 & 3 \\[1.1ex] -2 & 1 & 2 \\[1.1ex] 4 & -5 & 3 \end{vmatrix} = 3 \neq 0$

En cambio, la matriz A’ sí que contiene un determinante cuyo resultado es diferente de 0, de modo que la matriz A’ será de rango 3:

$\displaystyle rg(A')=3$

Por lo tanto, como el rango de la matriz A es más pequeño que el rango de la matriz A’, deducimos a partir del teorema de Rouché-Frobenius que se trata de un Sistema Incompatible (SI):

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = 2 \ \neq \ rg(A') = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SI}\phantom{^9_9}} \end{array}$

Ejercicios resueltos del teorema de Rouché – Frobenius

Ejercicio 1

Determina de qué tipo se trata el siguiente sistema de ecuaciones con 3 incógnitas mediante el teorema de Rouché-Frobenius:

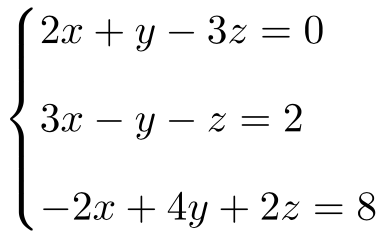
ejercicio resuelto del teorema de rouche - frobenius

Ver solución

Primero hacemos la matriz A y la matriz ampliada A’ del sistema:

$\displaystyle A= \left( \begin{array}{ccc} 2 & 1 & -3 \\[1.1ex] 3 & -1 & -1 \\[1.1ex] -2 & 4 & 2 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & -3 & 0 \\[1.1ex] 3 & -1 & -1 & 2 \\[1.1ex] -2 & 4 & 2 & 8 \end{array} \right)$

Ahora tenemos que hallar el rango de la matriz A. Para ello, miramos si el determinante de la matriz es diferente de 0:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & -3 \\[1.1ex] 3 & -1 & -1 \\[1.1ex] -2 & 4 & 2 \end{vmatrix} = -4+2-36+6+8-6=-30 \bm{\neq 0}$

Como la matriz tiene un determinante de tercer orden distinto de 0, la matriz A es de rango 3:

$\displaystyle rg(A)=3$

Una vez sabemos el rango de A, calculamos el rango de A’. Esta será como mínimo de rango 3, porque acabamos de ver que dentro tiene un determinante de orden 3 diferente de 0. A parte, no puede ser de rango 4, ya que no podemos hacer ningún determinante 4×4. Por tanto, la matriz A’ también es de rango 3:

$\displaystyle rg(A')=3$

Por tanto, gracias al teorema de Rouché-Frobenius sabemos que se trata de un Sistema Compatible Determinado (SCD), porque el rango de A es igual al rango de A’ y al número de incógnitas.

Ejercicio 2

Clasifica el siguiente sistema de ecuaciones con 3 incógnitas con el teorema de Rouché-Frobenius:

Ver solución

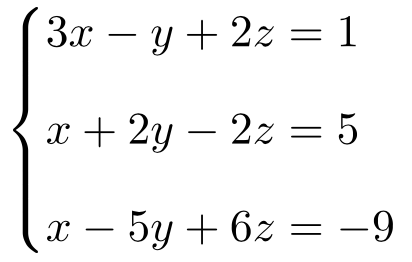
Antes de nada, construimos la matriz A y la matriz ampliada A’ del sistema:

$\displaystyle A= \left( \begin{array}{ccc}3 & -1 & 2 \\[1.1ex] 1 & 2 & -2 \\[1.1ex] 1 & -5 & 6 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 3 & -1 & 2 & 1 \\[1.1ex] 1 & 2 & -2 & 5 \\[1.1ex] 1 & -5 & 6 & -9 \end{array} \right)$

Ahora calculamos el rango de la matriz A:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 3 & -1 & 2 \\[1.1ex] 1 & 2 & -2 \\[1.1ex] 1 & -5 & 6 \end{vmatrix} = 0$

$\displaystyle \begin{vmatrix} 3 & -1 \\[1.1ex] 1 & 2 \end{vmatrix} = 7 \neq 0$

De manera que la matriz A es de rango 2:

$\displaystyle rg(A)=2$

Una vez sabemos el rango de A, calculamos el rango de A’. El determinante de las 3 primeras columnas ya sabemos que da 0, así que probamos con los otros determinantes 3×3 posibles:

$\displaystyle \begin{vmatrix}-1 & 2 & 1 \\[1.1ex] 2 & -2 & 5 \\[1.1ex] -5 & 6 & -9\end{vmatrix} = 0 \quad \begin{vmatrix}3 & 2 & 1 \\[1.1ex] 1 & -2 & 5 \\[1.1ex] 1 & 6 & -9\end{vmatrix} = 0 \quad \begin{vmatrix} 3 & -1 & 1 \\[1.1ex] 1 & 2 & 5 \\[1.1ex] 1 & -5 & -9\end{vmatrix} = 0$

Todos los determinantes 3×3 de la matriz A’ son 0, por tanto, la matriz A’ tampoco será de rango 3. Sin embargo, dentro sí que tiene determinantes de orden 2 diferentes de 0. Por ejemplo:

$\displaystyle \begin{vmatrix} -1 & 2 \\[1.1ex] 2 & -2 \end{vmatrix} = -2 \neq 0$

Así que la matriz A’ será de rango 2:

$\displaystyle rg(A')=2$

El rango de la matriz A es igual al rango de la matriz A’ pero estos dos son más pequeños que el número de incógnitas del sistema (3). Por lo tanto, por el teorema de Rouché-Frobenius sabemos que se trata de un Sistema Compatible Indeterminado (SCI):

Ejercicio 3

Determina de qué clase de sistema se trata el siguiente sistema de ecuaciones mediante el teorema de Rouché-Frobenius:

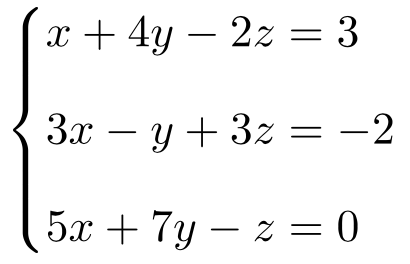
ejercicio resuelto paso a paso de teorema de rouche - frobenius

Ver solución

Primero hacemos la matriz A y la matriz ampliada A’ del sistema:

$\displaystyle A= \left( \begin{array}{ccc} 1 & 4 & -2 \\[1.1ex] 3 & -1 & 3 \\[1.1ex] 5 & 7 & -1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 4 & -2 & 3 \\[1.1ex] 3 & -1 & 3 & -2 \\[1.1ex] 5 & 7 & -1 & 0 \end{array} \right)$

Ahora calculamos el rango de la matriz A:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 4 & -2 \\[1.1ex] 3 & -1 & 3 \\[1.1ex] 5 & 7 & -1\end{vmatrix} = 0$

$\displaystyle \begin{vmatrix} 1 & 4 \\[1.1ex] 3 & -1 \end{vmatrix} = -13 \neq 0$

De modo que la matriz A es de rango 2:

$\displaystyle rg(A)=2$

Una vez sabemos el rango de A, calculamos el rango de A’. El determinante de las 3 primeras columnas ya sabemos que da 0, pero el determinante de las 3 últimas columnas no:

$\displaystyle \begin{vmatrix} 4 & -2 & 3 \\[1.1ex]-1 & 3 & -2 \\[1.1ex] 7 & -1 & 0 \end{vmatrix} = -40 \neq 0$

Por tanto, la matriz A’ es de rango 3:

$\displaystyle rg(A')=3$

El rango de la matriz A es más pequeño que el rango de la matriz A’, así que podemos deducir a partir del teorema de Rouché-Frobenius que se trata de un Sistema Incompatible (SI):

Ejercicio 4

Determina de qué tipo se trata el siguiente sistema de ecuaciones con 3 incógnitas mediante el teorema de Rouché-Frobenius:

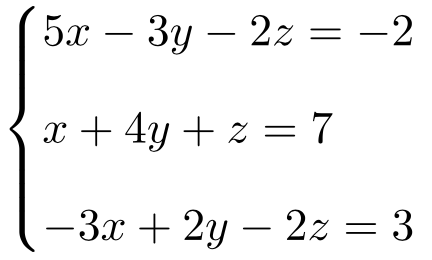
ejercicio resuelto de teorema de rouche - frobenius con 3 incogintas y 3 ecuaciones

Ver solución

Primero hacemos la matriz A y la matriz ampliada A’ del sistema:

$\displaystyle A= \left( \begin{array}{ccc} 5 & -3 & -2 \\[1.1ex] 1 & 4 & 1 \\[1.1ex]-3 & 2 & -2 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 5 & -3 & -2 & -2 \\[1.1ex] 1 & 4 & 1 & 7 \\[1.1ex]-3 & 2 & -2 & 3 \end{array} \right)$

Ahora tenemos que calcular el rango de la matriz A. Para ello, resolvemos el determinante de la matriz con la regla de Sarrus:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 5 & -3 & -2 \\[1.1ex] 1 & 4 & 1 \\[1.1ex]-3 & 2 & -2 \end{vmatrix} = -40+9-4-24-10-6=-75 \bm{\neq 0}$

Como la matriz tiene un determinante de tercer orden distinto de 0, la matriz A es de rango 3:

$\displaystyle rg(A)=3$

Por tanto, la matriz A’ también es de rango 3, ya que siempre es como mínimo del rango de A y no puede ser de rango 4 porque no podemos resolver ningún determinante 4×4.

$\displaystyle rg(A')=3$

Por tanto, gracias a la aplicación del teorema de Rouché-Frobenius sabemos que el sistema es un Sistema Compatible Determinado (SCD), porque el rango de A es igual al rango de A’ y al número de incógnitas.

Ejercicio 5

Identifica qué tipo de sistema es el siguiente sistema de ecuaciones a través el teorema de Rouché-Frobenius:

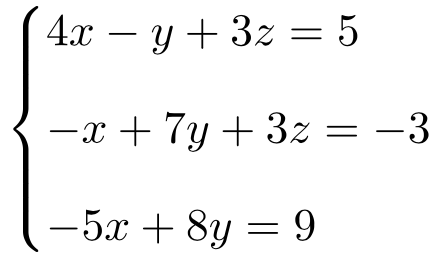
ejemplo del teorema de rouche - frobenius

Ver solución

Primero hacemos la matriz A y la matriz ampliada A’ del sistema:

$\displaystyle A= \left( \begin{array}{ccc} 4 & -1 & 3 \\[1.1ex] -1 & 7 & 3 \\[1.1ex] -5 & 8 & 0 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 4 & -1 & 3 & 5 \\[1.1ex] -1 & 7 & 3 & -3 \\[1.1ex] -5 & 8 & 0 & 9 \end{array} \right)$

Ahora calculamos el rango de la matriz A:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 4 & -1 & 3 \\[1.1ex] -1 & 7 & 3 \\[1.1ex] -5 & 8 & 0\end{vmatrix} = 0$

$\displaystyle \begin{vmatrix} 4 & -1 \\[1.1ex] -1 & 7 \end{vmatrix} = 27 \neq 0$

Por lo tanto, la matriz A es de rango 2:

$\displaystyle rg(A)=2$

Una vez sabemos el rango de A, calculamos el rango de A’. El determinante de las 3 primeras columnas ya sabemos que da 0, sin embargo el determinante de las 3 últimas columnas no:

$\displaystyle \begin{vmatrix} -1 & 3 & 5 \\[1.1ex] 7 & 3 & -3 \\[1.1ex] 8 & 0 & 9\end{vmatrix} = -408 \neq 0$

Por tanto, la matriz A’ es de rango 3:

$\displaystyle rg(A')=3$

Y, finalmente, aplicamos el rango el teorema de Rouché-Frobenius: el rango de la matriz A es más pequeño que el rango de la matriz A’, así que se trata de un Sistema Incompatible (SI):

Ejercicio 6

Clasifica el siguiente sistema de ecuaciones de orden 3 con el teorema de Rouché-Frobenius:

$\begin{cases} 6x-2y+4z=1 \\[1.5ex] -2x+4y+3z= 7 \\[1.5ex] 8x-6y+z = -6\end{cases}$

Ver solución

Primero de todo construimos la matriz A y la matriz ampliada A’ del sistema:

$\displaystyle A= \left( \begin{array}{ccc} 6 & -2 & 4 \\[1.1ex] -2 & 4 & 3 \\[1.1ex] 8 & -6 & 1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 6 & -2 & 4 & 1 \\[1.1ex] -2 & 4 & 3 & 7 \\[1.1ex] 8 & -6 & 1 & -6 \end{array} \right)$

Ahora calculamos el rango de la matriz A:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 6 & -2 & 4 \\[1.1ex] -2 & 4 & 3 \\[1.1ex] 8 & -6 & 1 \end{vmatrix} = 0$

$\displaystyle \begin{vmatrix} 6 & -2 \\[1.1ex] -2 & 4 \end{vmatrix} = 20 \neq 0$

De manera que la matriz A es de rango 2:

$\displaystyle rg(A)=2$

Una vez sabemos el rango de A, calculamos el rango de A’. El determinante de las 3 primeras columnas ya sabemos que da 0, así que probamos con los otros determinantes 3×3 posibles:

$\displaystyle \begin{vmatrix} -2 & 4 & 1 \\[1.1ex]4 & 3 & 7 \\[1.1ex] -6 & 1 & -6\end{vmatrix} = 0 \quad \begin{vmatrix}6 & 4 & 1 \\[1.1ex] -2 & 3 & 7 \\[1.1ex] 8 & 1 & -6\end{vmatrix} = 0 \quad \begin{vmatrix} 6 & -2 & 1 \\[1.1ex] -2 & 4 & 7 \\[1.1ex] 8 & -6 & -6\end{vmatrix} = 0$

Todos los determinantes 3×3 de la matriz A’ son 0, por tanto, la matriz A’ tampoco será de rango 3. Sin embargo, dentro sí que tiene determinantes de orden 2 diferentes de 0. Por ejemplo:

$\displaystyle \begin{vmatrix} 6 & -2 \\[1.1ex] -2 & 4 \end{vmatrix} = 20 \neq 0$

Así que la matriz A’ será de rango 2:

$\displaystyle rg(A')=2$

Por último, aplicando el teorema de Rouché-Frobenius, sabemos que es un Sistema Compatible Indeterminado (SCI), porque el rango de la matriz A es igual al rango de la matriz A’ pero estos dos son más pequeños que el número de incógnitas del sistema (3):

Teorema de Rouché – Frobenius

¿Qué es el teorema de Rouché – Frobenius?

Enunciado del teorema de Rouché-Frobenius

Ejemplo de Sistema Compatible Determinado (SCD)

Ejemplo de Sistema Compatible Indeterminado (SCI)

Ejemplo de Sistema Incompatible (SI)

Ejercicios resueltos del teorema de Rouché – Frobenius

Ejercicio 1

Ejercicio 2

Ejercicio 3

Ejercicio 4

Ejercicio 5

Ejercicio 6

Deja un comentario Cancelar respuesta