Resolver sistemas por la regla de Cramer (ejercicios resueltos)

En esta página verás qué es la regla de Cramer y, además, encontrarás ejemplos y ejercicios con resoluciones de sistemas de ecuaciones por la regla de Cramer.

Sumario

1. ¿Qué es la regla de Cramer?

2. Ejemplo 1: Sistema Compatible Determinado (SCD)

3. Ejemplo 2: Sistema Compatible Indeterminado (SCI)

4. Ejercicios resueltos de la regla de Cramer

¿Qué es la regla de Cramer?

La regla de Cramer es un método que se utiliza para resolver sistemas de ecuaciones por determinantes. Veamos cómo se utiliza:

Dado un sistema de ecuaciones:

$\begin{cases} ax+by+cz= \color{red}\bm{j} \\[1.5ex] dx+ey+fz=\color{red}\bm{k} \\[1.5ex] gx+hy+iz = \color{red}\bm{l} \end{cases}$

La matriz A y la matriz ampliada A’ del sistema son:

$\displaystyle A= \left( \begin{array}{ccc} a & b & c \\[1.1ex] d & e & f \\[1.1ex] g & h & i \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} a & b & c & \color{red}\bm{j} \\[1.1ex] d & e & f & \color{red}\bm{k} \\[1.1ex] g & h & i & \color{red}\bm{l} \end{array} \right)$

La regla de Cramer dice que la solución de un sistema de ecuaciones es:

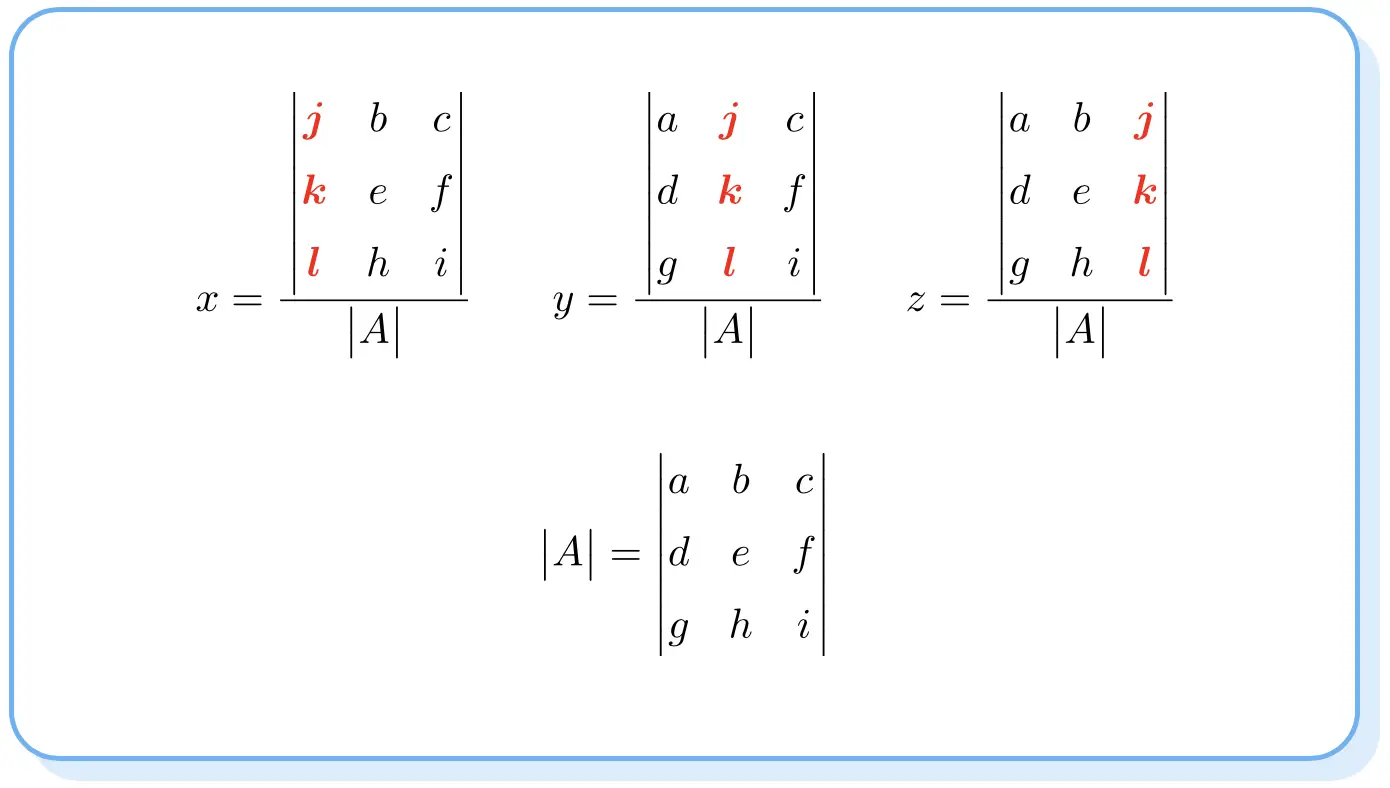
que es la regla de cramer, explicación de la regla de cramer

Fíjate que los determinantes de los numeradores son como el determinante de la matriz A pero cambiando la columna de cada incógnita por la columna de los términos independientes.

Por tanto, la regla de Cramer sirve para solucionar sistemas de ecuaciones lineales. Pero, como ya sabes, existen muchas maneras para resolver un sistema de ecuaciones, por ejemplo el metodo de Gauss Jordan es muy conocido.

A continuación tienes ejemplos de cómo resolver sistemas de ecuaciones lineales con la regla de Cramer, o a veces también escrito como regla de Kramer.

Ejemplo 1: Sistema Compatible Determinado (SCD)

Resuelve el siguiente sistema de 3 ecuaciones con 3 incógnitas utilizando la regla de Cramer:

$\begin{cases} 2x+y+3z= 1 \\[1.5ex] 3x-2y-z=0 \\[1.5ex] x+3y+2z = 5\end{cases}$

Primero de todo, hacemos la matriz A y la matriz ampliada A’ del sistema:

$\displaystyle A= \left( \begin{array}{ccc} 2 & 1 & 3 \\[1.1ex] 3 & -2 & -1 \\[1.1ex] 1 & 3 & 2\end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & 3 & 1 \\[1.1ex] 3 & -2 & -1 & 0 \\[1.1ex] 1 & 3 & 2 & 5 \end{array} \right)$

Ahora calculamos el rango de las dos matrices, con el objetivo de ver qué tipo de sistema es. Para calcular el rango de A, calculamos el determinante 3×3 de toda la matriz (con la regla de Sarrus) y miramos si da 0:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & 3 \\[1.1ex] 3 & -2 & -1 \\[1.1ex] 1 & 3 & 2\end{vmatrix} =-8-1+27+6+6-6 = 24 \neq 0$

El determinante de A es diferente de 0, por tanto, la matriz A es de rango 3.

$\displaystyle rg(A)=3$

De manera que la matriz A’ también es de rango 3, ya que no puede ser de rango 4 y tiene que ser como mínimo del mismo rango que la matriz A.

$\displaystyle rg(A')=3$

El rango de la matriz A es igual al rango de la matriz A’ y al número de incógnitas del sistema (3), por tanto, por el teorema de Rouché-Frobenius sabemos que se trata de un Sistema Compatible Determinado (SCD):

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 3 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}$

Una vez sabemos que el sistema es un SCD, aplicamos la regla de Cramer para resolverlo. Para ello recuerda que la matriz A, su determinante y la matriz A’ son:

$\displaystyle A= \left( \begin{array}{ccc} 2 & 1 & 3 \\[1.1ex] 3 & -2 & -1 \\[1.1ex] 1 & 3 & 2\end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & 3 & \color{red}\bm{1} \\[1.1ex] 3 & -2 & -1 & \color{red}\bm{0} \\[1.1ex] 1 & 3 & 2 & \color{red}\bm{5} \end{array} \right)$

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & 3 \\[1.1ex] 3 & -2 & -1 \\[1.1ex] 1 & 3 & 2\end{vmatrix} =24$

Para calcular la incógnita $\displaystyle x$ con la regla de Cramer, cambiamos la primera columna del determinante de A por la columna de términos independientes y lo dividimos entre el determinante de A:

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} \color{red}\bm{1} & 1 & 3 \\[1.1ex] \color{red}\bm{0} & -2 & -1 \\[1.1ex] \color{red}\bm{5} & 3 & 2 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{24}{24} = \bm{1}$

Para calcular la incógnita $\displaystyle y$ con la regla de Cramer, cambiamos la segunda columna del determinante de A por la columna de términos independientes y lo dividimos entre el determinante de A:

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix} 2 & \color{red}\bm{1} & 3 \\[1.1ex] 3 & \color{red}\bm{0} & -1 \\[1.1ex] 1 & \color{red}\bm{5} & 2\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{48}{24} = \bm{2}$

Para calcular $\displaystyle z$ con la regla de Cramer, cambiamos la tercera columna del determinante de A por la columna de términos independientes y lo dividimos entre el determinante de A:

$\displaystyle \bm{z} = \cfrac{\begin{vmatrix} 2 & 1 & \color{red}\bm{1} \\[1.1ex] 3 & -2 & \color{red}\bm{0} \\[1.1ex] 1 & 3 & \color{red}\bm{5}\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-24}{24} = \bm{-1}$

Por lo tanto, la solución del sistema de ecuaciones es:

$\displaystyle \bm{x = 1 \qquad y=2 \qquad z = -1}$

Ejemplo 2: Sistema Compatible Indeterminado (SCI)

Resuelve el siguiente sistema de ecuaciones con la regla de Cramer:

$\begin{cases} 3x+2y+4z=1 \\[1.5ex] -2x+3y-z=0 \\[1.5ex] x+5y+3z = 1 \end{cases}$

Primero de todo, hacemos la matriz A y la matriz ampliada A’ del sistema:

$\displaystyle A= \left( \begin{array}{ccc} 3 & 2 & 4 \\[1.1ex] -2 & 3 & -1 \\[1.1ex] 1 & 5 & 3 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 3 & 2 & 4 & 1 \\[1.1ex] -2 & 3 & -1 & 0 \\[1.1ex] 1 & 5 & 3 & 1 \end{array} \right)$

Ahora calculamos el rango de las dos matrices, y así poder ver de qué tipo de sistema se trata. Para calcular el rango de A, calculamos el determinante de toda la matriz (con la regla de Sarrus) y miramos si es 0:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 3 & 2 & 4 \\[1.1ex] -2 & 3 & -1 \\[1.1ex] 1 & 5 & 3\end{vmatrix} = 27-2-40-12+15+12= 0$

El determinante da 0, por tanto, la matriz A no es de rango 3. Pero sí que tiene algún determinante 2×2 diferente de 0:

$\displaystyle \begin{vmatrix} 3 & 2 \\[1.1ex] -2 & 3 \end{vmatrix} =9-(-4)=13\neq 0$

De manera que la matriz A es de rango 2:

$\displaystyle rg(A)=2$

Una vez sabemos el rango de la matriz A, calculamos el de la matriz A’. El determinante de las 3 primeras columnas da 0, así que probamos con los otros determinantes 3×3 posibles dentro de la matriz A’:

$\displaystyle \begin{vmatrix} 2 & 4 & 1 \\[1.1ex] 3 & -1 & 0 \\[1.1ex] 5 & 3 & 1 \end{vmatrix} = 0 \qquad \begin{vmatrix} 3 & 4 & 1 \\[1.1ex] -2 & -1 & 0 \\[1.1ex] 1 & 3 & 1 \end{vmatrix} = 0 \qquad \begin{vmatrix} 3 & 2 & 1 \\[1.1ex] -2 & 3 & 0 \\[1.1ex] 1 & 5 & 1 \end{vmatrix} = 0$

Todos los determinantes de orden 3 dan 0. Pero, evidentemente, la matriz A’ tiene el mismo determinante 2×2 distinto de 0 que la matriz A:

$\displaystyle \begin{vmatrix} 3 & 2 \\[1.1ex] -2 & 3 \end{vmatrix} =9-(-4)=13\neq 0$

Por tanto, la matriz A’ también es de rango 2:

$\displaystyle rg(A')=2$

Por lo tanto, como el rango de la matriz A es igual al rango de la matriz A’ pero estos dos son más pequeños que el número de incógnitas del sistema (3), sabemos por el teorema de Rouché-Frobenius que se trata de un Sistema Compatible Indeterminado (SCI):

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = 2 \ < \ n =3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCI}\phantom{^9_9}} \end{array}$

Cuando queremos resolver un Sistema Compatible Indeterminado (SCI) tenemos que transformar el sistema: primero eliminamos una ecuación, después convertimos una variable en λ (normalmente la variable z), y finalmente ponemos los términos con λ junto con los términos independientes.

Una vez hemos transformado el sistema, aplicamos la regla de Cramer y obtendremos la solución del sistema en función de λ.

En este caso, eliminaremos la última ecuación del sistema:

$\begin{cases} 3x+2y+4z=1 \\[1.5ex] -2x+3y-z=0 \\[1.5ex]\cancel{x+5y+3z = 1} \end{cases} \longrightarrow \quad \begin{cases} 3x+2y+4z=1 \\[1.5ex] -2x+3y-z=0\end{cases}$

Ahora convertimos la variable z en λ:

$\begin{cases} 3x+2y+4z=1 \\[1.5ex] -2x+3y-z=0 \end{cases} \xrightarrow{z \ = \ \lambda}\quad \begin{cases} 3x+2y+4\lambda=1 \\[1.5ex] -2x+3y-\lambda=0\end{cases}$

Y ponemos los términos con λ junto con los términos independientes:

$\begin{cases} 3x+2y=1-4\lambda \\[1.5ex] -2x+3y=\lambda \end{cases}$

Por tanto, la matriz A y la matriz A’ del sistema quedan:

$\displaystyle A= \left( \begin{array}{ccc} 3 & 2 \\[1.1ex] -2 & 3 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 3 & 2 & 1 -4\lambda \\[1.1ex] -2 & 3 & \lambda \end{array} \right)$

Finalmente, una vez hemos transformado el sistema, aplicamos la regla de Cramer. Así que resolvemos el determinante de A:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 3 & 2 \\[1.1ex] -2 & 3\end{vmatrix} = 13$

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 1 -4\lambda & 2 \\[1.1ex] \lambda & 3 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{3(1-4\lambda) -2\lambda}{13} = \cfrac{\bm{3-14\lambda} }{\bm{13}}$

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix} 3 & 1 -4\lambda \\[1.1ex]-2& \lambda \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{3\lambda -\bigl(-2(1-4\lambda)\bigr)}{13}= \cfrac{3\lambda -\bigl(-2+8\lambda\bigr)}{13} = \cfrac{\bm{2-5\lambda} }{\bm{13}}$

De modo que la solución del sistema de ecuaciones queda en función de λ, ya que es un SCI y, por tanto, tiene infinitas soluciones:

$\displaystyle \bm{x =} \cfrac{\bm{3-14\lambda} }{\bm{13}} \qquad \bm{y=}\cfrac{\bm{2-5\lambda} }{\bm{13}} \qquad \bm{z = \lambda}$

Ejercicios resueltos de la regla de Cramer

Ejercicio 1

Aplicar la regla de Cramer para resolver el siguiente sistema de dos ecuaciones con 2 incógnitas:

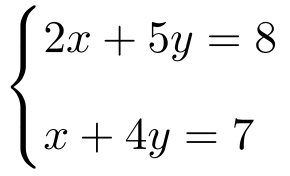
ejercicio resuelto paso a paso con la regla de cramer 2x2

Ver solución

Lo primero que debemos hacer es la matriz A y la matriz ampliada A’ del sistema:

$\displaystyle A= \left( \begin{array}{cc} 2 & 5 \\[1.1ex] 1 & 4 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 2 & 5 & 8 \\[1.1ex] 1 & 4 & 7 \end{array}\right)$

Ahora tenemos que hallar el rango de la matriz A. Para ello, miramos si el determinante de toda la matriz es diferente de 0:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 5 \\[1.1ex] 1 & 4 \end{vmatrix} = 8-5=3 \bm{\neq 0}$

Como la matriz tiene un determinante 2×2 distinto de 0, la matriz A es de rango 2:

$\displaystyle rg(A)=2$

Una vez sabemos el rango de A, calculamos el rango de A’. Esta será como mínimo de rango 2, porque acabamos de ver que dentro tiene un determinante de orden 2 diferente de 0. A parte, no puede ser de rango 3, ya que no podemos hacer ningún determinante 3×3. Por tanto, la matriz A’ también es de rango 2:

$\displaystyle rg(A')=2$

Por tanto, aplicando el teorema de Rouché-Frobenius sabemos que se trata de un Sistema Compatible Determinado (SCD), porque el rango de A es igual al rango de A’ y al número de incógnitas.

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 2 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 2 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}$

Una vez sabemos que el sistema es un SCD, aplicamos la regla de Cramer para resolverlo.

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 8 & 5 \\[1.1ex] 7 & 4\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-3}{3} = \bm{-1}$

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix}2 & 8 \\[1.1ex] 1 & 7\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{6}{3} = \bm{2}$

Por lo tanto, la solución del sistema de ecuaciones es:

$\displaystyle \bm{x = -1 \qquad y=2}$

Ejercicio 2

Halla la solución del siguiente sistema de tres ecuaciones con 3 incógnitas por la regla de Cramer:

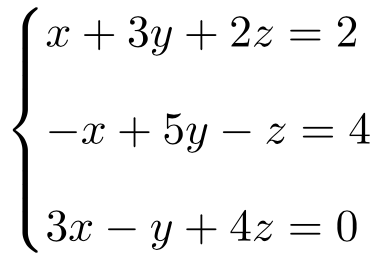
ejercicio resuelto de la regla de cramer de un sistema de ecuaciones 3x3

Ver solución

Primero de todo hacemos la matriz A y la matriz ampliada A’ del sistema:

$\displaystyle A= \left( \begin{array}{ccc} 1 & 3 & 2\\[1.1ex] -1 & 5 & -1\\[1.1ex] 3 & -1 & 4 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 3 & 2 & 2 \\[1.1ex] -1 & 5 & -1 & 4 \\[1.1ex] 3 & -1 & 4 & 0 \end{array}\right)$

Ahora hallamos el rango de la matriz A calculando el determinante de la matriz 3×3 con la regla de Sarrus:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 3 & 2 \\[1.1ex] -1 & 5 & -1\\[1.1ex] 3 & -1 & 4 \end{vmatrix} = 20-9+2-30-1+12=-6 \bm{\neq 0}$

Como la matriz tiene un determinante de orden 3 distinto de 0, la matriz A es de rango 3:

$\displaystyle rg(A)=3$

En consecuencia, la matriz A’ también es de rango 3:

$\displaystyle rg(A')=3$

Por tanto, utilizando el teorema de Rouché-Frobenius sabemos que se trata de un Sistema Compatible Determinado (SCD), porque el rango de A es igual al rango de A’ y al número de incógnitas.

Una vez sabemos que el sistema es un SCD, tenemos que aplicar la regla de Cramer para resolver el sistema.

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 2 & 3 & 2 \\[1.1ex] 4 & 5 & -1\\[1.1ex]0 & -1 & 4\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-18}{-6} = \bm{3}$

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix}1 & 2 & 2 \\[1.1ex] -1 & 4 & -1\\[1.1ex] 3 & 0 & 4\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-6}{-6} = \bm{1}$

Para calcular $\displaystyle z$ con la regla de Cramer, cambiamos la tercera columna del determinante de A por la columna de términos independientes y lo dividimos entre el determinante de A:

$\displaystyle \bm{z} = \cfrac{\begin{vmatrix} 1 & 3 & 2 \\[1.1ex] -1 & 5 & 4 \\[1.1ex] 3 & -1 & 0\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{12}{-6} = \bm{-2}$

Por lo tanto, la solución del sistema de ecuaciones es:

$\displaystyle \bm{x =3 \qquad y=1 \qquad z=-2}$

Ejercicio 3

Calcula la solución del siguiente sistema de tres ecuaciones con 3 incógnitas por la regla de Cramer:

Ver solución

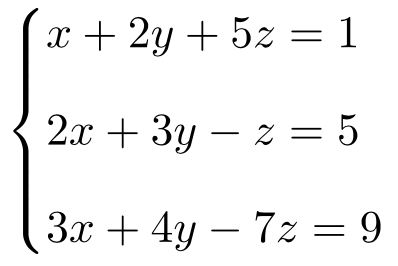
Primero hacemos la matriz A y la matriz ampliada A’ del sistema:

$\displaystyle A= \left( \begin{array}{ccc} 1 & 2 & 5\\[1.1ex] 2 & 3 & -1 \\[1.1ex] 3 & 4 & -7 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 2 & 5 & 1 \\[1.1ex] 2 & 3 & -1 & 5 \\[1.1ex] 3 & 4 & -7 & 9 \end{array}\right)$

Calculamos el rango de la matriz A:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 2 & 5\\[1.1ex] 2 & 3 & -1 \\[1.1ex] 3 & 4 & -7 \end{vmatrix} =-21-6+40-45+4+28=0$

$\displaystyle \begin{vmatrix} 1 & 2 \\[1.1ex] 2 & 3 \end{vmatrix} = 3-4 = -1 \neq 0$

$\displaystyle rg(A)=2$

$\displaystyle \begin{vmatrix} 2 & 5 & 1 \\[1.1ex] 3 & -1 & 5 \\[1.1ex] 4 & -7 & 9 \end{vmatrix} = 0 \qquad \begin{vmatrix} 1 & 5 & 1 \\[1.1ex] 2 & -1 & 5 \\[1.1ex] 3 & -7 & 9\end{vmatrix} = 0 \qquad \begin{vmatrix} 1 & 2 & 1 \\[1.1ex] 2 & 3 & 5 \\[1.1ex] 3 & 4 & 9 \end{vmatrix} = 0$

Todos los determinantes de orden 3 dan 0. Sin embargo, la matriz A’ tiene el mismo determinante 2×2 distinto de 0 que la matriz A:

$\displaystyle \begin{vmatrix} 1 & 2 \\[1.1ex] 2 & 3 \end{vmatrix} = 3-4 = -1 \neq 0$

Por tanto, la matriz A’ también es de rango 2:

$\displaystyle rg(A')=2$

Como el rango de la matriz A es igual al rango de la matriz A’ pero estos dos son más pequeños que el número de incógnitas del sistema (3), sabemos por el teorema de Rouché-Frobenius que se trata de un Sistema Compatible Indeterminado (SCI):

Al ser una sistema SCI, debemos eliminar una ecuación. En este caso, eliminaremos la última ecuación del sistema:

$\begin{cases} x+2y+5z=1 \\[1.5ex] 2x+3y-z=5 \\[1.5ex]\cancel{3x+4y-7z = 9} \end{cases} \longrightarrow \quad \begin{cases} x+2y+5z=1 \\[1.5ex] 2x+3y-z=5\end{cases}$

Ahora convertimos la variable z en λ:

$\begin{cases} x+2y+5z=1 \\[1.5ex] 2x+3y-z=5 \end{cases} \xrightarrow{z \ = \ \lambda}\quad \begin{cases} x+2y+5\lambda=1 \\[1.5ex] 2x+3y-\lambda=5\end{cases}$

Y ponemos los términos con λ junto con los términos independientes:

$\begin{cases} x+2y=1-5\lambda\\[1.5ex] 2x+3y=5+\lambda \end{cases}$

De manera que la matriz A y la matriz A’ del sistema quedan:

$\displaystyle A= \left( \begin{array}{ccc} 1 & 2 \\[1.1ex] 2 & 3 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 1 & 2 & 1 -5\lambda \\[1.1ex] 2 & 3 &5+\lambda \end{array} \right)$

Finalmente, una vez hemos transformado el sistema, aplicamos la regla de Cramer. Así que resolvemos el determinante de A:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 2 \\[1.1ex] 2 & 3\end{vmatrix} =-1$

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 1-5\lambda & 2 \\[1.1ex] 5+\lambda & 3 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{3-15\lambda -(10+2\lambda)}{-1} = \cfrac{-7-17\lambda}{-1} = \bm{7+17\lambda}$

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix} 1 & 1-5\lambda \\[1.1ex] 2 & 5+\lambda \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{5+\lambda -(2-10\lambda)}{-1}= \cfrac{3+11\lambda}{-1} = \bm{-3-11\lambda}$

De modo que la solución del sistema de ecuaciones queda en función de λ, ya que es un SCI y, por tanto, tiene infinitas soluciones:

$\displaystyle \bm{x =7+17\lambda} \qquad \bm{y=-3-11\lambda} \qquad \bm{z = \lambda}$

Ejercicio 4

Resuelve el siguiente problema de un sistema de tres ecuaciones con 3 incógnitas aplicando la regla de Cramer:

$\begin{cases} -2x+5y+z=8 \\[1.5ex] 6x+2y+4z=4 \\[1.5ex] 3x-2y+z = -2 \end{cases}$

Ver solución

En primer lugar, hacemos la matriz A y la matriz ampliada A’ del sistema:

$\displaystyle A= \left( \begin{array}{ccc}-2 & 5 & 1 \\[1.1ex] 6 & 2 & 4 \\[1.1ex] 3 & -2 & 1\end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} -2 & 5 & 1 & 8 \\[1.1ex] 6 & 2 & 4 & 4 \\[1.1ex] 3 & -2 & 1 & -2 \end{array}\right)$

Ahora calculamos el rango de la matriz A calculando el determinante de la matriz 3×3 mediante la regla de Sarrus:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} -2 & 5 & 1 \\[1.1ex] 6 & 2 & 4 \\[1.1ex] 3 & -2 & 1 \end{vmatrix} = -4+60-12-6-16-30=-8 \bm{\neq 0}$

Como la matriz tiene un determinante de orden 3 distinto de 0, la matriz A es de rango 3:

$\displaystyle rg(A)=3$

En consecuencia, la matriz A’ también es de rango 3, ya que esta tiene que ser como mínimo del mismo rango que la matriz A y no puede ser de rango 4 porque es una matriz de dimensión 3×4.

$\displaystyle rg(A')=3$

Por tanto, usando el teorema de Rouché-Frobenius deducimos que se trata de un Sistema Compatible Determinado (SCD), porque el rango de A es igual al rango de A’ y al número de incógnitas.

Una vez sabemos que el sistema es un SCD, tenemos que aplicar la regla de Cramer para resolver el sistema.

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 8 & 5 & 1 \\[1.1ex] 4 & 2 & 4 \\[1.1ex] -2 & -2 & 1\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{16}{-8} = \bm{-2}$

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix}-2 & 8 & 1 \\[1.1ex] 6 & 4 & 4 \\[1.1ex] 3 & -2 & 1\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{0}{-6} = \bm{0}$

Para calcular $\displaystyle z$ con la regla de Cramer, cambiamos la tercera columna del determinante de A por la columna de términos independientes y lo dividimos entre el determinante de A:

$\displaystyle \bm{z} = \cfrac{\begin{vmatrix} -2 & 5 & 8 \\[1.1ex] 6 & 2 & 4 \\[1.1ex] 3 & -2 & -2\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-32}{-8} = \bm{4}$

Por lo tanto, la solución del sistema de ecuaciones lineales es:

$\displaystyle \bm{x =-2 \qquad y=0 \qquad z=4}$

Ejercicio 5

Resuelve el siguiente sistema de ecuaciones lineales por la regla de Cramer:

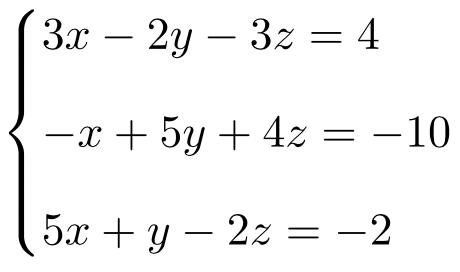
ejemplo de como resolver un sistema de ecuaciones con la regla de cramer

Ver solución

Primero de todo hacemos la matriz A y la matriz ampliada A’ del sistema:

$\displaystyle A= \left( \begin{array}{ccc} 3 & -2 & -3 \\[1.1ex] -1 & 5 & 4 \\[1.1ex] 5 & 1 & -2 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 3 & -2 & -3 & 4 \\[1.1ex] -1 & 5 & 4 & -10 \\[1.1ex] 5 & 1 & -2 & -2 \end{array}\right)$

Calculamos el rango de la matriz A:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 3 & -2 & -3 \\[1.1ex] -1 & 5 & 4 \\[1.1ex] 5 & 1 & -2 \end{vmatrix} =-30-40+3+75-12+4=0$

$\displaystyle \begin{vmatrix} 3 & -2 \\[1.1ex] -1 & 5 \end{vmatrix} = 15- (2)= 13 \neq 0$

$\displaystyle rg(A)=2$

$\displaystyle \begin{vmatrix} -2 & -3 & 4 \\[1.1ex] 5 & 4 & -10 \\[1.1ex] 1 & -2 & -2 \end{vmatrix} = 0 \qquad \begin{vmatrix}3 & -3 & 4 \\[1.1ex] -1 & 4 & -10 \\[1.1ex] 5 & -2 & -2\end{vmatrix} = 0 \qquad \begin{vmatrix} 3 & -2 & 4 \\[1.1ex] -1 & 5 & -10 \\[1.1ex] 5 & 1 &-2\end{vmatrix} = 0$

Todos los determinantes de orden 3 dan 0. Pero, obviamente, la matriz A’ tiene el mismo determinante de orden 2 distinto de 0 que la matriz A:

$\displaystyle \begin{vmatrix} 3 & -2 \\[1.1ex] -1 & 5 \end{vmatrix} = 13 \neq 0$

Por lo tanto, la matriz A’ también es de rango 2:

$\displaystyle rg(A')=2$

El rango de la matriz A es igual al rango de la matriz A’ pero estos dos son más pequeños que el número de incógnitas del sistema (3), así que por el teorema de Rouché-Frobenius sabemos que es un Sistema Compatible Indeterminado (SCI):

Al ser una sistema SCI, debemos eliminar una ecuación. En este caso, eliminaremos la última ecuación del sistema:

$\begin{cases} 3x-2y-3z=4 \\[1.5ex] -x+5y+4z=-10 \\[1.5ex]\cancel{5x+y-2z = -2} \end{cases} \longrightarrow \quad \begin{cases} 3x-2y-3z=4 \\[1.5ex] -x+5y+4z=-10\end{cases}$

Ahora convertimos la variable z en λ:

$\begin{cases} 3x-2y-3z=4 \\[1.5ex] -x+5y+4z=-10 \end{cases} \xrightarrow{z \ = \ \lambda}\quad \begin{cases} 3x-2y-3\lambda=4 \\[1.5ex] -x+5y+4\lambda=-10\end{cases}$

Y ponemos los términos con λ junto con los términos independientes:

$\begin{cases} 3x-2y=4+3\lambda \\[1.5ex] -x+5y=-10-4\lambda\end{cases}$

De manera que la matriz A y la matriz A’ del sistema quedan:

$\displaystyle A= \left( \begin{array}{ccc} 3 & -2 \\[1.1ex] -1 & 5 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 3 & -2 & 4+3\lambda \\[1.1ex] 1 & 5 &-10-4\lambda \end{array} \right)$

Finalmente, una vez hemos transformado el sistema, aplicamos la regla de Cramer. Así que resolvemos el determinante de A:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix}3& -2 \\[1.1ex] -1 & 5\end{vmatrix} =13$

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 4+3\lambda & -2 \\[1.1ex]-10-4\lambda & 5\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{20+15\lambda -(20+8\lambda)}{13} = \cfrac{\bm{7\lambda}}{\bm{13}}$

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix} 3 & 4+3\lambda \\[1.1ex] -1 & -10-4\lambda\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-30-12\lambda -(-4-3\lambda)}{13}= \cfrac{\bm{-26-9\lambda}}{\bm{13}}$

De manera que la solución del sistema de ecuaciones queda en función de λ, ya que es un SCI y, por tanto, el sistema tiene infinitas soluciones:

$\displaystyle \bm{x=} \cfrac{\bm{7\lambda}}{\bm{13}} \qquad \bm{y=} \cfrac{\bm{-26-9\lambda}}{\bm{13}} \qquad \bm{z = \lambda}$

10 comentarios en “Regla de Cramer”

Javier
22/02/2021 a las 01:14

¡Excelente contenido, me ha ayudado mucho a poder estudiar!

Responder
1. Matrices y Determinantes
  22/02/2021 a las 13:17
  
  ¡Gracias Javier! ¡Nos alegra haberte podido ayudar!
  
  Responder
john g
21/09/2021 a las 03:47

quien me puede ayudar con este problema
Una fábrica de plásticos produce envases hechos a partir de diferentes Tipos de plásticos. Con base en Bioplásticos, biodegradables y técnicos, el propietario necesita producir un envase combinado que cueste $3.25 por libra fabricado. El costo por libra de estos Tipos de plásticos es de $4.00, $3.00 y $2.00, respectivamente. La cantidad de técnicos debe ser la misma que la cantidad de biodegradables. ¿Cuánto de cada Tipo de plástico debe tener el envase final?

Responder
1. Matrices y Determinantes
  30/09/2021 a las 09:46
  
  Hola John,
  
  Para resolver este problema necesitas más datos. Ahora solo se podrían plantear dos ecuaciones y el problema tiene tres incógnitas, por lo que es un sistema SCI.
  
  Responder
  1. Nikhol
    02/11/2021 a las 20:47
    
    Por favor me ayudan paso a paso
    -4x+5y+3z=38
    
    Responder
    1. Matrices y Determinantes
      04/11/2021 a las 20:45
      
      Hola Nikhol,
      
      Para poder utilizar la regla de Cramer necesitas tener como mínimo un sistema con dos ecuaciones.
      
      Responder
hilario
16/01/2022 a las 05:47

√3/2𝑋 + 2𝑌 + 𝑍 = 0
(ln 𝑒)𝑋 + 𝑆𝑒𝑛(45)𝑌 −2/3𝑍 = 4!
-X +Y –Z = 0

como hago para calcular los 2 valores que no tengo

Responder
1. Matrices y Determinantes
  19/01/2022 a las 11:47
  
  Hola Hilario, de hecho tienes tres valores desconocidos, ya que el sistema de ecuaciones tiene tres incógnitas.
  
  La raíz, el logaritmo natural de e, el seno de 45º y las fracciones en realidad son números, solo tienes que hallar su valor con la calculadora y luego puedes aplicar el método de Cramer como si fuera un sistema de ecuaciones normal.
  
  Responder
Marcos Campos
06/04/2022 a las 22:19

Hola.

Se puede utilizar la regla de Cramer cuando tenemos un sistema incompatible?

Gracias.

Responder
1. Matrices y Determinantes
  16/04/2022 a las 08:35
  
  Hola Marcos,
  
  Puedes utilizar la regla de Cramer, pero no obtendrás ningún resultado del sistema de ecuaciones.
  
  Al ser un sistema de ecuaciones incompatible, el determinante de la matriz A dará 0, por lo que no conseguirás ninguna solución con las fórmulas de la regla de Cramer. De hecho, un sistema incompatible no tiene solución.
  
  Responder

¿Qué es la regla de Cramer?

Ejemplo 1: Sistema Compatible Determinado (SCD)

Ejemplo 2: Sistema Compatible Indeterminado (SCI)

Ejercicios resueltos de la regla de Cramer

Ejercicio 1

Ejercicio 2

Ejercicio 3

Ejercicio 4

Ejercicio 5

10 comentarios en “Regla de Cramer”

Deja un comentario Cancelar respuesta