▷ Cómo multiplicar matrices (ejercicios resueltos)

En esta página veremos cómo hacer una multiplicación de matrices de dimensión 2×2, 3×3, 4×4, etc. Te explicamos el procedimiento de multiplicar matrices paso a paso a través de un ejemplo, y después encontrarás ejercicios resueltos para que también puedas practicar. Finalmente, aprenderás cuándo no se pueden multiplicar dos matrices y todas las propiedades de esta operación de matrices.

Sumario

1. ¿Cómo multiplicar dos matrices?

2. Ejercicios resueltos de multiplicaciones de matrices

3. ¿Cuándo no se pueden multiplicar dos matrices?

4. Propiedades de la multiplicación de matrices

¿Cómo multiplicar dos matrices?

Vamos a ver el procedimiento de cómo hacer la multiplicación de dos matrices con un ejemplo:

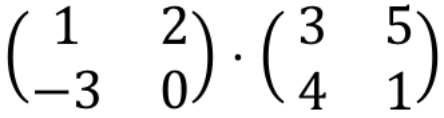
Para calcular una multiplicación de matrices se deben multiplicar las filas de la matriz de la izquierda por las columnas de la matriz de la derecha.

Por tanto, primero tenemos que multiplicar la primera fila por la primera columna. Para ello, multiplicamos uno a uno cada elemento de la primera fila por cada elemento de la primera columna, y sumamos los resultados. De manera que todo esto será el primer elemento de la primera fila de la matriz resultante. Fíjate en el procedimiento:

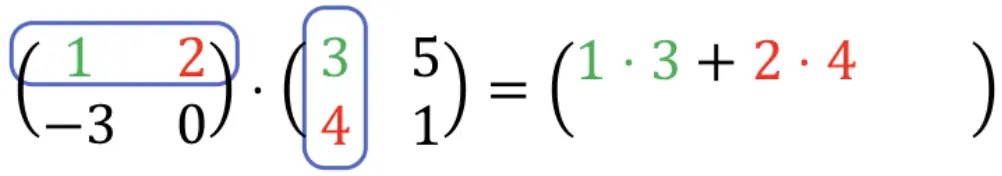
como resolver una multiplicacion de matrices 2x2 , operaciones con matrices

1⋅3 + 2⋅4 = 3 + 8 = 11. Por tanto:

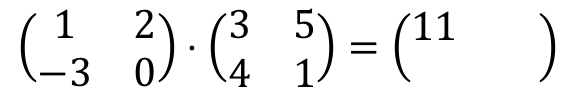
resolver una multiplicación de matrices 2x2

Ahora nos toca multiplicar la primera fila por la segunda columna. Así que repetimos el procedimiento: multiplicamos uno a uno cada elemento de la primera fila por cada elemento de la segunda columna, y sumamos los resultados. Y todo esto será el segundo elemento de la primera fila de la matriz resultante:

cómo hacer una multiplicación de matrices de dimensión 2

1⋅5 + 2⋅1 = 5 + 2 = 7. Por tanto:

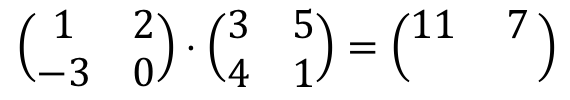
procedimiento de cómo multiplicar dos matrices de orden 2

Una vez tenemos la primera fila de la matriz resultante llena, pasamos a la segunda fila. Así que multiplicamos la segunda fila por la primera columna repitiendo el procedimiento: multiplicamos uno a uno cada elemento de la segunda fila por cada elemento de la primera columna, y sumamos los resultados:

-3⋅3 + 0⋅4 = -9 + 0 = -9. Por tanto:

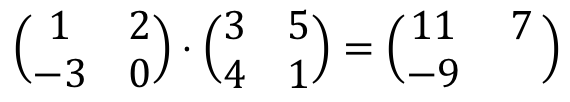
Por último, multiplicamos la segunda fila por la segunda columna. Siempre con el mismo procedimiento: multiplicamos uno a uno cada elemento de la segunda fila por cada elemento de la segunda columna, y sumamos los resultados:

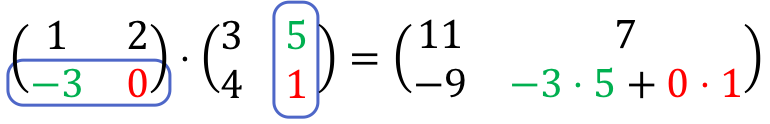
cómo resolver el producto de dos matrices 2x2

-3⋅5 + 0⋅1 = -15 + 0 = -15. Por tanto:

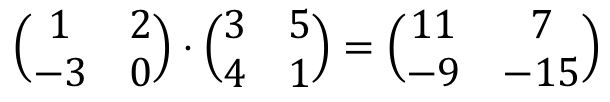
ejercicio resuelto de multiplicación de matrices 2x2

Y aquí termina la multiplicación de las dos matrices. Como has visto, se tienen que multiplicar las filas por las columnas repitiendo siempre el mismo procedimiento: multiplicamos uno a uno cada elemento de la fila por cada elemento de la columna, y sumamos los resultados.

Ejercicios resueltos de multiplicaciones de matrices

Ejercicio 1

Resuelve el siguiente producto matricial:

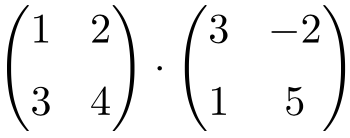
ejercicio resuelto paso a paso de producto de matrices 2x2 , operaciones con matrices

Ver solución

Se trata de un producto de matrices de orden 2:

$\displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix}$

Para resolver un producto matricial debemos multiplicar las filas de la matriz de la izquierda por las columnas de la matriz de la derecha.

Por tanto, primero multiplicamos la primera fila por la primera columna. Para ello, multiplicamos uno a uno cada elemento de la primera fila por cada elemento de la primera columna, y sumamos los resultados. Y todo esto será el primer elemento de la primera fila de la matriz resultante:

$\displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix} = \begin{pmatrix} 1\cdot 3 +2 \cdot 1 & \\[1.1ex] & \end{pmatrix} = \begin{pmatrix} 5 & \\[1.1ex] & \end{pmatrix}$

Ahora multiplicamos la primera fila por la segunda columna, para obtener el segundo elemento de la primera fila de la matriz resultante:

$\displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix} = \begin{pmatrix} -1 & 1\cdot (-2) +2 \cdot 5 \\[1.1ex] & \end{pmatrix} = \begin{pmatrix}5 & 8 \\[1.1ex] & \end{pmatrix}$

Pasamos a la segunda fila, por tanto, multiplicamos la segunda fila por la primera columna:

$\displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix} = \begin{pmatrix} -1 & 8 \\[1.1ex] 3\cdot 3 +4 \cdot 1 & \end{pmatrix}= \begin{pmatrix}5 & 8 \\[1.1ex] 13 & \end{pmatrix}$

Finalmente, multiplicamos la segunda fila por la segunda columna, para calcular el último elemento de la matriz:

$\displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix}= \begin{pmatrix} -1 & 8 \\[1.1ex]1 & 3\cdot (-2) +4 \cdot 5 \end{pmatrix}=\begin{pmatrix} 5 & 8 \\[1.1ex] 13 & 14 \end{pmatrix}$

Así que el resultado de la multiplicación de matrices es:

$\displaystyle \begin{pmatrix} \bm{5} & \bm{8} \\[1.1ex]\bm{13} & \bm{14} \end{pmatrix}$

Ejercicio 2

Halla el resultado de la siguiente multiplicación de matrices cuadradas 2×2:

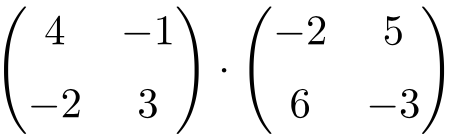
ejercicio resuelto paso a paso de multiplicacion de matrices 2x2 , operaciones de matrices

Ver solución

Se trata de un producto de matrices de dimensión 2×2.

Para resolver la multiplicación, tenemos que multiplicar las filas de la matriz de la izquierda por las columnas de la matriz de la derecha:

$\displaystyle \begin{aligned} \begin{pmatrix} 4 & -1 \\[1.1ex] -2 & 3 \end{pmatrix} \cdot \begin{pmatrix} -2 & 5 \\[1.1ex] 6 & -3 \end{pmatrix} & = \begin{pmatrix} 4\cdot (-2)+(-1) \cdot 6 & 4\cdot 5+(-1) \cdot (-3) \\[1.1ex](-2)\cdot (-2)+3 \cdot 6 & (-2)\cdot 5+3 \cdot (-3)\end{pmatrix} \\[2ex] & =\begin{pmatrix} \bm{-14} & \bm{23} \\[1.1ex]\bm{22} & \bm{-19} \end{pmatrix} \end{aligned}$

Ejercicio 3

Calcula la siguiente multiplicación matricial 3×3:

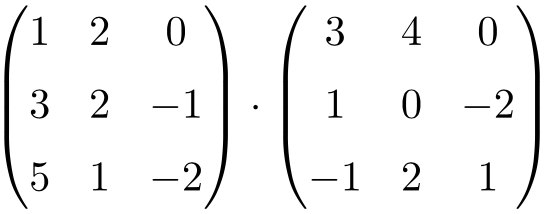
ejercicio resuelto paso a paso de multiplicacion de matrices 3x3 , operaciones de matrices

Ver solución

Para hacer la multiplicación de matrices 3×3, debemos multiplicar las filas de la matriz de la izquierda por las columnas de la matriz de la derecha:

$\displaystyle \begin{array}{l} \begin{pmatrix} 1 & 2 & 0 \\[1.1ex] 3 & 2 & -1 \\[1.1ex] 5 & 1 & -2 \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 & 0 \\[1.1ex] 1 & 0 & -2 \\[1.1ex] -1 & 2 & 1 \end{pmatrix} = \\[7.5ex] =\begin{pmatrix} 1 \cdot 3+2 \cdot 1+ 0 \cdot (-1) & 1 \cdot 4+2 \cdot 0+ 0 \cdot 2 & 1 \cdot 0+2 \cdot (-2)+ 0 \cdot 1 \\[1.1ex] 3 \cdot 3+2 \cdot 1+ (-1) \cdot (-1) & 3 \cdot 4+2 \cdot 0+ (-1) \cdot 2 & 3 \cdot 0+2 \cdot (-2)+ (-1) \cdot 1 \\[1.1ex] 5 \cdot 3+1 \cdot 1+ (-2) \cdot (-1) & 5 \cdot 4+1 \cdot 0+ (-2) \cdot 2 & 5 \cdot 0+1 \cdot (-2)+ (-2) \cdot 1 \end{pmatrix} = \\[7.5ex] =\begin{pmatrix} \bm{5} & \bm{4} & \bm{-4} \\[1.1ex] \bm{12} & \bm{10} & \bm{-5} \\[1.1ex] \bm{18} & \bm{16} & \bm{-4} \end{pmatrix}\end{array}$

Ejercicio 4

Dada la matriz $A$ :

$\displaystyle A= \begin{pmatrix} 3 & 1 & -2 \\[1.1ex] 4 & 2 & -1 \end{pmatrix}$

Calcula:

$\displaystyle 2A\cdot A^t$

Ver solución

Primero calcularemos la matriz traspuesta de $A$ para poder hacer la multiplicación. Y para hacer la matriz traspuesta tenemos que cambiar las filas por columnas. Es decir, la primera fila de la matriz pasa a ser la primera columna de la matriz, y la segunda fila de la matriz pasa a ser la segunda columna de la matriz. Por tanto:

$\displaystyle A^t= \begin{pmatrix} 3 & 4 \\[1.1ex] 1 & 2 \\[1.1ex] -2 & -1 \end{pmatrix}$

Así que la operación de matrices queda:

$\displaystyle 2A\cdot A^t = 2 \begin{pmatrix} 3 & 1 & -2 \\[1.1ex] 4 & 2 & -1 \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 \\[1.1ex] 1 & 2 \\[1.1ex] -2 & -1 \end{pmatrix}$

Ahora ya podemos hacer los cálculos. Calculamos primero $2A$ (aunque también se podría calcular primero $A \cdot A^t$ ):

$\displaystyle \begin{pmatrix} 2 \cdot 3 & 2 \cdot 1 & 2 \cdot (-2) \\[1.1ex] 2 \cdot 4 & 2 \cdot 2 & 2 \cdot (-1) \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 \\[1.1ex] 1 & 2 \\[1.1ex] -2 & -1 \end{pmatrix} =$

$\displaystyle =\begin{pmatrix} 6 & 2 & -4 \\[1.1ex] 8 & 4 & -2 \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 \\[1.1ex] 1 & 2 \\[1.1ex] -2 & -1 \end{pmatrix}$

Y, por último, resolvemos el producto de matrices:

$\displaystyle \begin{pmatrix} 6 \cdot 3 +2 \cdot 1 + (-4) \cdot (-2) & 6 \cdot 4 +2 \cdot 2 + (-4) \cdot (-1) \\[1.1ex] 8 \cdot 3 +4 \cdot 1 + (-2) \cdot (-2) & 8 \cdot 4 +4 \cdot 2 + (-2) \cdot (-1) \end{pmatrix} =$

$\displaystyle = \begin{pmatrix} \bm{28} & \bm{32} \\[1.1ex]\bm{32} & \bm{42} \end{pmatrix}$

Ejercicio 5

Dadas las siguientes matrices:

$\displaystyle A=\begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix} \qquad B=\begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix}$

Calcula:

$\displaystyle A\cdot B - B \cdot A$

Ver solución

Se trata de una operación que combina una resta junto con multiplicaciones de matrices de orden 2:

$\displaystyle A\cdot B - B \cdot A= \begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix}\cdot \begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix} - \begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix} \cdot \begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix}$

Calculamos primero la multiplicación de la izquierda:

$\displaystyle \begin{pmatrix} 2\cdot (-1) + 4 \cdot 3 & 2\cdot (-2) + 4 \cdot (-3) \\[1.1ex] (-3)\cdot (-1) + 5 \cdot 3 & (-3)\cdot (-2) + 5 \cdot (-3) \end{pmatrix} - \begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix} \cdot \begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix} =$

$\displaystyle= \begin{pmatrix} 10 & -16 \\[1.1ex] 18 & -9 \end{pmatrix} - \begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix} \cdot \begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix}$

Ahora resolvemos la multiplicación de la derecha:

$\displaystyle \begin{pmatrix} 10 & -16 \\[1.1ex] 18 & -9 \end{pmatrix} - \begin{pmatrix} -1 \cdot 2 +(-2) \cdot (-3) & -1 \cdot 4 +(-2) \cdot 5 \\[1.1ex]3 \cdot 2 +(-3) \cdot (-3) & 3 \cdot 4 +(-3) \cdot 5 \end{pmatrix} =$

$\displaystyle =\begin{pmatrix} 10 & -16 \\[1.1ex] 18 & -9 \end{pmatrix} - \begin{pmatrix} 4 &-14 \\[1.1ex]15 & -3 \end{pmatrix}$

Y finalmente restamos las matrices:

$\displaystyle \begin{pmatrix} 10-4 & -16 -(-14) \\[1.1ex] 18-15 & -9-(-3) \end{pmatrix} =$

$\displaystyle =\begin{pmatrix} \bm{6} & \bm{-2} \\[1.1ex] \bm{3} & \bm{-6} \end{pmatrix}$

¿Cuándo no se pueden multiplicar dos matrices?

No se pueden multiplicar todas las matrices. Para poder multiplicar dos matrices el número de columnas de la primera matriz debe coincidir con el número de filas de la segunda matriz.

Por ejemplo, la siguiente multiplicación no se puede realizar por que la primera matriz tiene 3 columnas y, en cambio, la segunda matriz tiene 2 filas:

$\displaystyle\begin{pmatrix} 1 & 3 & -2 \\[1.1ex] 4 & 0 & 5 \end{pmatrix} \cdot \begin{pmatrix} 2 & 1 \\[1.1ex] 3 & -1 \end{pmatrix} \ \longleftarrow \ \color{red} \bm{\times}$

Pero si invertimos el orden, sí que se pueden multiplicar. Porque la primera matriz tiene dos columnas y la segunda matriz dos filas:

$\displaystyle \begin{aligned} \begin{pmatrix} 2 & 1 \\[1.1ex] 3 & -1 \end{pmatrix} \cdot \begin{pmatrix} 1 & 3 & -2 \\[1.1ex] 4 & 0 & 5 \end{pmatrix} & = \begin{pmatrix} 2\cdot 1 + 1 \cdot 4 & 2\cdot 3 + 1 \cdot 0 & 2\cdot (-2) + 1 \cdot 5 \\[1.1ex] 3\cdot 1 + (-1) \cdot 4 & 3\cdot 3 + (-1) \cdot 0 & 3\cdot (-2) + (-1) \cdot 5 \end{pmatrix} \\[2ex] & = \begin{pmatrix} \bm{6} & \bm{6} & \bm{1} \\[1.1ex]\bm{-1} & \bm{9} & \bm{-11} \end{pmatrix} \end{aligned}$

Propiedades de la multiplicación de matrices

Este tipo de operación matricial tiene las siguientes características:

La multiplicación de matrices es asociativa:

$\displaystyle \left( A \cdot B \right) \cdot C = A \cdot \left( B \cdot C \right)$

La multiplicación de matrices también tiene la propiedad distributiva:

$\displaystyle A\cdot \left(B+C\right) = A\cdot B + A \cdot C$

El producto de matrices no es conmutativo:

$\displaystyle A \cdot B \neq B \cdot A$

Por ejemplo, la siguiente multiplicación de matrices da un resultado:

$\displaystyle \begin{aligned} \begin{pmatrix} 1 & -1 \\[1.1ex] 2 & 3 \end{pmatrix} \cdot \begin{pmatrix} -2 & 5 \\[1.1ex] 0 & 1 \end{pmatrix} & = \begin{pmatrix} 1\cdot (-2) + (-1) \cdot 0 & 1\cdot 5 + (-1) \cdot 1 \\[1.1ex] 2\cdot (-2) + 3 \cdot 0 & 2\cdot 5 + 3 \cdot 1 \end{pmatrix} \\[2ex] & = \begin{pmatrix} \bm{-2} & \bm{4} \\[1.1ex] \bm{-4} & \bm{13} \end{pmatrix}\end{aligned}$

Pero el resultado del producto es diferente si invertimos el orden de multiplicación de las matrices:

$\displaystyle \begin{aligned}\begin{pmatrix} -2 & 5 \\[1.1ex] 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} 1 & -1 \\[1.1ex] 2 & 3 \end{pmatrix} & = \begin{pmatrix} -2 \cdot 1 + 5\cdot 2 & -2 \cdot (-1) + 5\cdot 3 \\[1.1ex] 0 \cdot 1 + 1\cdot 2 & 0 \cdot (-1) + 1\cdot 3 \end{pmatrix} \\[2ex] & = \begin{pmatrix} \bm{8} & \bm{17} \\[1.1ex] \bm{2} & \bm{3} \end{pmatrix}\end{aligned}$

Además, cualquier matriz multiplicada por la matriz identidad da como resultado la misma matriz. A esto se le llama propiedad de la identidad multiplicativa:

$\displaystyle A \cdot I=A$

$\displaystyle I \cdot A=A$

Por ejemplo:

$\displaystyle \begin{pmatrix} 2 & 7 \\[1.1ex] -6 & 5 \end{pmatrix} \cdot \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix} = \begin{pmatrix} \bm{2} & \bm{7} \\[1.1ex] \bm{-6} & \bm{5} \end{pmatrix}$

Finalmente, como ya te estarás imaginando, cualquier matriz multiplicada por la matriz nula es igual a la matriz nula. A esto se le llama propiedad multiplicativa de cero:

$\displaystyle A \cdot 0=0$

$\displaystyle 0\cdot A=0$

Por ejemplo:

$\displaystyle \begin{pmatrix} 6 & -4 \\[1.1ex] 3 & 8 \end{pmatrix} \cdot \begin{pmatrix} 0 & 0 \\[1.1ex] 0 & 0 \end{pmatrix} = \begin{pmatrix} \bm{0} & \bm{0} \\[1.1ex] \bm{0} & \bm{0}\end{pmatrix}$

13 comentarios en “Multiplicación de matrices”

MILAGROS
08/09/2020 a las 01:48

MUY CHEVERE.. PARA DEMASIADO BÁSICO PERO ES LA BASE PARA APRENDER LO SIGUIENTE… MUCHAS GRACIAS Y ESPERO QUE TE ENCUETRES BIEN DE SALUD EN ESTA PANDEMIS…! SALUDOS.

Responder
1. Matrices y Determinantes
  10/09/2020 a las 10:56
  
  ¡Muchas gracias! En Matrices y Determinantes siempre intentamos hacer cada artículo lo mejor posible.
  Gracias por preocuparte y desde aquí te deseamos lo mejor, tanto en salud como en tu vida personal. 😉
  
  Responder
Augusto
01/10/2020 a las 19:33

magnifica las explicaciones y la composición de las páginas

enhorabuena por un trabajo bien hecho

Responder
1. marc.gisbert@matricesydeterminantes.com
  01/10/2020 a las 19:44
  
  ¡Muchas gracias Augusto! ¡Recibir este tipo de felicitaciones nos motiva a continuar con el proyecto!
  
  Responder
Lewis
17/03/2021 a las 23:09

Se puede multiplicar una matriz de 2×3 por otra de 2×3

Responder
1. Matrices y Determinantes
  20/03/2021 a las 00:12
  
  Hola Lewis,
  
  Para poder calcular la multiplicación entre dos matrices el número de columnas de la primera matriz debe ser igual al número de filas de la segunda matriz.
  
  En este caso, la primera matriz tiene tres columnas y la segunda matriz dos filas, por lo tanto, no se pueden multiplicar entre sí.
  
  Este es un ejemplo de dos matrices con la misma dimensión pero que no se pueden multiplicar entre sí.
  
  Responder
ferney nieto s
08/10/2021 a las 04:23

Muchas gracias por esta explicación tan clara la verdad hasta hora estoy empezando este tema, pero me fue muy útil

Responder
1. Matrices y Determinantes
  11/10/2021 a las 13:27
  
  ¡Me alegro de que sirva Ferney! ¡Muchas gracias!
  
  Responder
Brisa
19/07/2022 a las 05:09

¡Su explicación y la composición didáctica de la página son realmente muy buenas!

Responder
1. Matrices y Determinantes
  22/07/2022 a las 09:13
  
  ¡Muchísimas gracias Brisa! <3
  
  Responder
juleiny
05/07/2023 a las 06:17

muchisimas gr4acias me ayudo mucho . me perdi la clase de matrices y estaba muy perdida . pero esta informacion bien explicada me ayudo mucho

Responder
1. Matrices y Determinantes
  31/07/2023 a las 23:04
  
  ¡Muchas gracias Juleiny!
  
  Responder
yariel
17/10/2023 a las 15:23

esta pagina es muy eficiente y muy buena

Responder

¿Cómo multiplicar dos matrices?

Ejercicios resueltos de multiplicaciones de matrices

Ejercicio 1

Ejercicio 2

Ejercicio 3

Ejercicio 4

Ejercicio 5

¿Cuándo no se pueden multiplicar dos matrices?

Propiedades de la multiplicación de matrices

13 comentarios en “Multiplicación de matrices”

Deja un comentario Cancelar respuesta