Definición de matriz y tipos de matrices

En este post te explicamos qué son las matrices y cómo se determina la dimensión de una matriz. Además, podrás ver ejemplos de matrices. Y, finalmente, encontrarás cuáles son los tipos de matrices más importantes.

Sumario
1. ¿Qué es una matriz?
2. Ejemplos de matrices
3. Dimensión de una matriz
4. Tipos de matrices
4.1. Matriz fila
4.2. Matriz columna
4.3. Matriz traspuesta
4.4. Matriz cuadrada
4.5. Matriz triangular
4.6. Matriz diagonal
4.7. Matriz escalar
4.8. Matriz identidad o unidad
4.9. Matriz nula
4.10. Matriz simétrica
4.11. Matriz antisimétrica

¿Qué es una matriz?

Una matriz de orden m \times n es un conjunto de números dispuestos en m  filas y n columnas:

\displaystyle A =\left( \begin{array}{cccc} a_{11} & a_{12} & \cdots & a_{1n} \\[1.1ex] a_{21} & a_{22} & \cdots & a_{2n} \\[1.1ex] \vdots & \vdots & \ddots & \vdots \\[1.1ex] a_{m1} & a_{m2} & \cdots & a_{mn} \end{array} \right)

Ejemplos de matrices

A continuación, puedes ver varios ejemplos de matrices diferentes:

\displaystyle A = \begin{pmatrix} 2 & -1 & 0 \\[1.1ex] 1 & 4 & -3 \\[1.1ex] -2 & 8 & 7 \end{pmatrix} \qquad B = \begin{pmatrix} 9 & 2 \\[1.1ex] 5 & 6 \end{pmatrix} \qquad C = \begin{pmatrix} 5 & 2 & -3 \\[1.1ex] 2 & 1 & 8 \end{pmatrix}

Dimensión de una matriz

La dimensión de una matriz es \bm{m \times n} . Donde m  corresponde al número de filas de la matriz, y n  al número de columnas.

Ejemplos:

matriz de dimensión 2 \times 3:

\displaystyle \begin{pmatrix} 1 & 2 & 5 \\[1.1ex] -1 & 3 & 4 \end{pmatrix}

matriz de dimensión 2 \times 1 :

\displaystyle \begin{pmatrix} 5 \\[1.1ex] 2 \end{pmatrix}

Tipos de matrices

A continuación te explicamos las características de los tipos de matrices más importantes.

Matriz fila

Es aquella matriz que solo tiene 1 fila:

\displaystyle\begin{pmatrix} 3 & 6 & -2 \end{pmatrix}

Matriz columna

Es aquella matriz que solo tiene 1 columna:

\displaystyle \begin{pmatrix} 6 \\[1.1ex] 4 \end{pmatrix}

Matriz traspuesta

La matriz traspuesta o transpuesta es la matriz que se obtiene al cambiar las filas por columnas. Y se representa poniendo una «t» arriba a la derecha de la matriz \left(A^t \right) .

Ejemplos:

\displaystyle A= \begin{pmatrix} 2 & 3 \\[1.1ex] -1 & 5 \end{pmatrix} \ \longrightarrow \ A^t= \begin{pmatrix} 2 & -1 \\[1.1ex] 3 & 5 \end{pmatrix}

\displaystyle B= \begin{pmatrix} 1 & 5 & 4 \\[1.1ex] 3 & 0 & 2 \end{pmatrix} \ \longrightarrow \ B^t= \begin{pmatrix} 1 & 3 \\[1.1ex] 5 & 0 \\[1.1ex] 4 & 2 \end{pmatrix}

Matriz cuadrada

Una matriz cuadrada es una matriz que tiene el mismo número de filas que de columnas (m=n ) .

Por ejemplo, una matriz cuadrada de orden 3 sería:

\displaystyle \left( \begin{array}{ccc} 1 & 6 & 3 \\[1.1ex] 2 & 4 & 0 \\[1.1ex] 5 & -1 & 2 \end{array} \right)

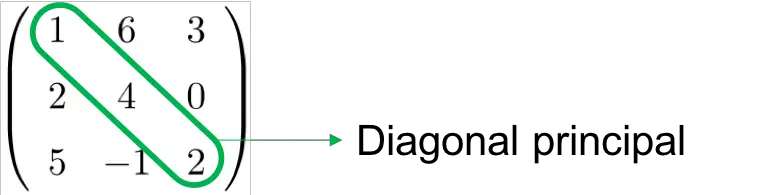
La diagonal principal de una matriz cuadrada son los elementos que van desde la esquina superior izquierda hasta la esquina inferior derecha:

diagonal principal de una matriz cuadrada

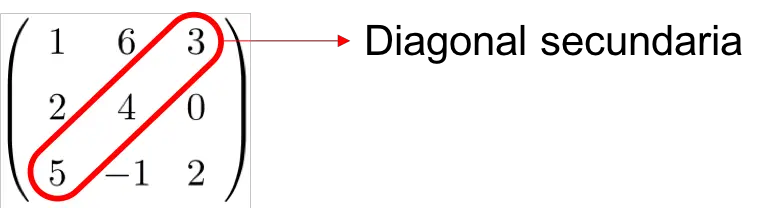
La diagonal secundaria de una matriz cuadrada son los elementos que van desde la esquina inferior izquierda hasta la esquina superior derecha:

diagonal secundaria de una matriz cuadrada

Te recomendamos que veas todas las propiedades de las matrices cuadradas, ya que seguramente son el tipo de matrices que más se utilizan y, por tanto, son muy importantes para el álgebra lineal.

Matriz triangular

Una matriz triangular es aquella matriz en la que todos los elementos por encima o por debajo de la diagonal principal son 0.

Las matrices triangulares se dividen en dos tipos: las matrices triangulares superiores, cuyos elementos por debajo de la diagonal principal son cero, y las matrices triangulares inferiores, cuyos elementos por encima de la diagonal principal son cero. Para entender del todo las diferencias entre ellas, puedes consultar más ejemplos de matrices triangulares.

Matriz triangular superior:

\displaystyle \begin{pmatrix} 4 & 1 & 7 \\[1.1ex] 0 & 2 & 5 \\[1.1ex] 0 & 0 & 3 \end{pmatrix}

Matriz triangular inferior:

\displaystyle \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 2 & 3 & 0 \\[1.1ex] -1 & 2 & 4 \end{pmatrix}

Matriz diagonal

Una matriz diagonal es una matriz cuadrada en la que todos los elementos que no estén situados en la diagonal principal son ceros. Puedes ver las propiedades y más ejemplos de matrices diagonales en este enlace.

\displaystyle \begin{pmatrix} 4 & 0 & 0 \\[1.1ex] 0 & 2 & 0 \\[1.1ex] 0 & 0 & -3 \end{pmatrix}

Aunque estas matrices parecen muy simples porque tienen muchos 0s, en realidad son muy importantes para las matemáticas. De hecho, existe todo un procedimiento para diagonalizar una matriz, de modo que las matrices diagonalizables tienen una gran importancia.

Matriz escalar

Una matriz escalar es una matriz diagonal en la que todos los elementos de la diagonal principal son iguales. Si quieres puedes ver aquí más ejemplos de matrices escalares.

\displaystyle \begin{pmatrix} 4 & 0 & 0 \\[1.1ex] 0 & 4 & 0 \\[1.1ex] 0 & 0 & 4 \end{pmatrix}

Matriz identidad o unidad

La matriz identidad es una matriz diagonal en la que todos los elementos de la diagonal principal son 1.

\displaystyle \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}

Como toda matriz diagonal, parece un tipo de matriz muy sencillo. Pero que no te engañe su apariencia, es una matriz muy utilizada debido a sus propiedades, por ejemplo se usa para invertir una matriz. Te recomendamos que veas las propiedades de la matriz identidad para que puedas comprender cuánto de útil es.

Matriz nula

Una matriz nula es una matriz en la que todos sus elementos son 0:

\displaystyle \begin{pmatrix} 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \end{pmatrix}

Como puedes ver, esta matriz no es nada compleja. Pero aunque no lo parezca, tiene su utilidad. Puedes ver sus aplicaciones en la página de las propiedades de la matriz nula.

Matriz simétrica

Una matriz simétrica es una matriz en la que la diagonal principal es un eje de simetría.

\displaystyle \begin{pmatrix} 2 & 3 & -1 \\[1.1ex] 3 & 5 & 9 \\[1.1ex] -1 & 9 & 1 \end{pmatrix}

Debido a las propiedades de las matrices simétricas, el resultado de trasponer una matriz simétrica es la propia matriz.

Matriz antisimétrica

Una matriz antisimétrica es una matriz en la que la diagonal principal está llena de ceros y, además, es un eje de antisimetría.

\displaystyle \begin{pmatrix} 0 & 4 & 2 \\[1.1ex] -4 & 0 & -3 \\[1.1ex] -2 & 3 & 0 \end{pmatrix}

En el siguiente enlace puedes ver todas las propiedades y más ejemplos de matrices antisimétricas.

Ahora que has visto los tipos de matrices, seguro que te estás preguntando… ¿y para qué sirve todo esto? Pues una de las principales aplicaciones son las operaciones de matrices, siendo la más importante de ellas la multiplicación, que también puedes ver cómo se hace en la página de matrices multiplicación.

12 comentarios en “Definición de matriz y tipos de matrices”

      1. ING. Walter a bolivar h

        Gracias por tu aportación . Refresqué lo que estudie en 1971-73 . Estoy prepandome para dibujar 3D por coordenadas x,y,z en CAD , dados 8 puntos , dibujar un arquitectónico con muros y losa dado el espesor de muros .

        Responder
        1. Matrices y Determinantes

          ¡Muchas gracias Walter!

          Siempre es buen momento para retomar las matemáticas. ¡Mucha suerte en tu nuevo proyecto! 😉

          Responder

Deja un comentario

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *

Ir arriba