Cómo calcular la suma y la resta de matrices

En esta página veremos cómo hacer una suma y una resta de matrices. Además tienes ejemplos que te ayudarán a entenderlo perfectamente y ejercicios resueltos para que puedas practicar. También encontrarás todas las propiedades de la suma de matrices.

Sumario
1. ¿Cómo hacer una suma y una resta de matrices?
2. Ejemplos:
3. Ejercicios resueltos de sumas y restas de matrices
4. Propiedades de la suma de matrices

¿Cómo hacer una suma y una resta de matrices?

Para calcular una suma (o resta) de dos matrices se tienen que sumar (o restar) los elementos que ocupan la misma posición en las matrices.

Ejemplos:

ejemplos de suma y resta de matrices 2x2 , operaciones con matrices

Fíjate que para poder sumar o restar dos matrices, estas deben tener la misma dimensión. Por ejemplo, las siguientes matrices no se pueden sumar porque la primera es una matriz de dimensión 2×2 y la segunda es una matriz de dimensión 3×2:

\displaystyle \begin{pmatrix} 1 & 3 \\[1.1ex] 0 & 2 \end{pmatrix} + \begin{pmatrix} 5 & 6 \\[1.1ex] -2 & 4 \\[1.1ex] 7 & 1 \end{pmatrix} \ \longleftarrow \ \color{red} \bm{\times}}

Ejercicios resueltos de sumas y restas de matrices

Ejercicio 1

Calcula la siguiente suma de matrices 2×2:

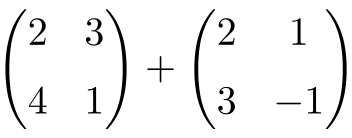
ejercicio resuelto paso a paso de suma de matrices 2x2

Se trata de una suma de dos matrices cuadradas de dimensión 2×2:

\displaystyle \begin{pmatrix} 2 & 3 \\[1.1ex] 4 & 1 \end{pmatrix} + \begin{pmatrix} 2 & 1 \\[1.1ex] 3 & -1 \end{pmatrix} = \begin{pmatrix} 2+2 & 3+1 \\[1.1ex] 4+3 & 1+(-1) \end{pmatrix} = \begin{pmatrix} \bm{4} & \bm{4} \\[1.1ex] \bm{7} & \bm{0} \end{pmatrix}

 

Ejercicio 2

Realiza la siguiente resta de matrices:

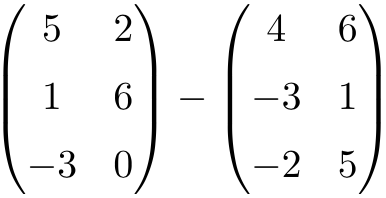
ejercicio resuelto paso a paso de resta de matrices , operaciones con matrices

Se trata de una resta de dos matrices de dimensión 3×2:

\displaystyle \begin{pmatrix} 5 & 2 \\[1.1ex] 1 & 6 \\[1.1ex] -3 & 0 \end{pmatrix} - \begin{pmatrix} 4 & 6 \\[1.1ex] -3 & 1 \\[1.1ex]-2 & 5 \end{pmatrix} = \begin{pmatrix} 5-4 & 2-6 \\[1.1ex] 1-(-3) & 6-1 \\[1.1ex] -3-(-2) & 0-5 \end{pmatrix} = \begin{pmatrix} \bm{1}& \bm{-4} \\[1.1ex] \bm{4} & \bm{5} \\[1.1ex] \bm{-1} & \bm{-5} \end{pmatrix}

 

Ejercicio 3

Halla el resultado de la siguiente suma matricial de dimensión 3×3:

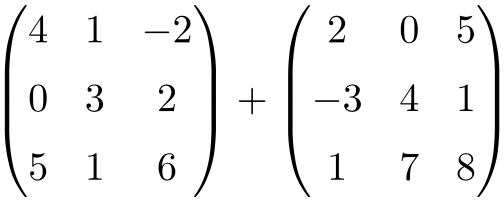
ejercicio resuelto paso a paso de suma de matrices 3x3 , operaciones con matrices

Se trata de una suma de dos matrices cuadradas de orden 3×3:

\displaystyle \begin{pmatrix} 4 & 1 & -2 \\[1.1ex] 0 & 3 & 2 \\[1.1ex] 5 & 1 & 6 \end{pmatrix} + \begin{pmatrix} 2 & 0 & 5 \\[1.1ex] -3 & 4 & 1 \\[1.1ex] 1 & 7 & 8 \end{pmatrix} = \begin{pmatrix} 4+2 & 1+0 & -2+5 \\[1.1ex] 0+(-3) & 3+4 & 2+1 \\[1.1ex] 5+1 & 1+7 & 6+8 \end{pmatrix} = \begin{pmatrix} \bm{6}& \bm{1} & \bm{3} \\[1.1ex] \bm{-3} & \bm{7} & \bm{3} \\[1.1ex] \bm{6} & \bm{8} & \bm{14} \end{pmatrix}

 

Ejercicio 4

Calcula la siguiente suma y resta de matrices cuadradas de orden 2:

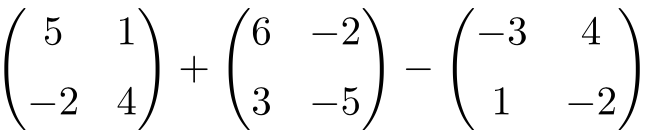
ejercicio resuelto paso a paso de suma y resta de matrices 2x2 , operaciones con matrices

Se trata de una operación combinada con una suma y una resta de matrices cuadradas de orden 2:

\displaystyle \begin{pmatrix} 5 & 1 \\[1.1ex] -2 & 4 \end{pmatrix} + \begin{pmatrix} 6 & -2 \\[1.1ex] 3 & -5 \end{pmatrix} -\begin{pmatrix} -3 & 4 \\[1.1ex] 1 & -2 \end{pmatrix}

Así que primero sumamos las matrices de la izquierda:

\displaystyle \begin{pmatrix} 11 & -1 \\[1.1ex] 1 & -1 \end{pmatrix} -\begin{pmatrix} -3 & 4 \\[1.1ex] 1 & -2 \end{pmatrix}

Y luego calculamos la resta de matrices:

\displaystyle \begin{pmatrix} \bm{14} & \bm{-5} \\[1.1ex] \bm{0} & \bm{1} \end{pmatrix}

 

Ejercicio 5

Resuelve la siguiente suma y resta matricial:

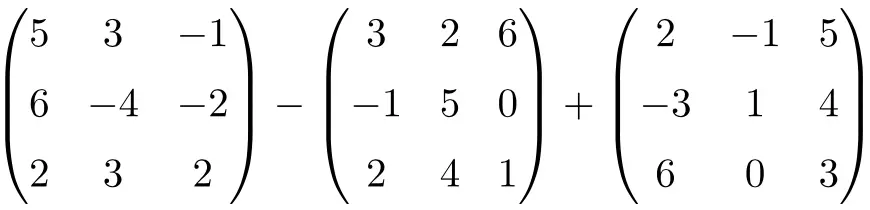
ejercicio resuelto paso a paso de suma y resta de matrices 3x3 , operaciones con matrices

Se trata de una operación combinada de una resta y una suma de matrices cuadradas de orden 3:

\displaystyle \begin{pmatrix}5 & 3 & -1 \\[1.1ex] 6 & -4 & -2 \\[1.1ex] 2 & 3 & 2 \end{pmatrix}-\begin{pmatrix} 3 & 2 & 6 \\[1.1ex]-1 & 5 & 0 \\[1.1ex] 2 & 4 & 1 \end{pmatrix} + \begin{pmatrix}2 & -1 & 5 \\[1.1ex] -3 & 1 & 4 \\[1.1ex] 6 & 0 & 3 \end{pmatrix}

En primer lugar, resolvemos la resta de matrices:

\displaystyle \begin{pmatrix}2 & 1 & -7 \\[1.1ex] 7 & -9 & -2 \\[1.1ex] 0 & -1 & 1 \end{pmatrix}+\begin{pmatrix}2 & -1 & 5 \\[1.1ex] -3 & 1 & 4 \\[1.1ex] 6 & 0 & 3 \end{pmatrix}

Y finalmente hacemos la suma de matrices:

\displaystyle \begin{pmatrix} \bm{4} & \bm{0} & \bm{-2} \\[1.1ex] \bm{4} & \bm{-8} & \bm{2} \\[1.1ex] \bm{6} & \bm{-1} & \bm{4} \end{pmatrix}

 

Ahora que ya sabes cómo sumar y restar matrices, es un buen momento para ver cómo multiplicar matrices, seguramente la más importante de las operaciones con matrices. También encontrarás ejercicios resueltos paso a paso de multiplicaciones de matrices para que puedas practicar, como en todas las páginas de esta web. 😉

Propiedades de la suma de matrices

La adición matricial cumple con las siguientes características:

  • La suma de matrices tiene la propiedad conmutativa:

\displaystyle A +B = B + A

Por tanto, es igual el orden con el que sumamos las matrices. Para demostrarlo sumaremos dos matrices cambiando su orden y ya verás como el resultado es el mismo.

Así que procedemos a sumar dos matrices en un determinado orden:

\displaystyle \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & -1 \end{pmatrix} + \begin{pmatrix} 4 & 1 \\[1.1ex] 5 & 2 \end{pmatrix}= \begin{pmatrix} \bm{5} & \bm{4} \\[1.1ex] \bm{7} & \bm{1} \end{pmatrix}

Fíjate que si invertimos el orden de la suma de las matrices, el resultado sigue siendo el mismo:

\displaystyle \begin{pmatrix} 4 & 1 \\[1.1ex] 5 & 2 \end{pmatrix} + \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & -1 \end{pmatrix}= \begin{pmatrix} \bm{5} & \bm{4} \\[1.1ex] \bm{7} & \bm{1} \end{pmatrix}

 
  • Otra propiedad de la suma de matrices es la del elemento opuesto:

\displaystyle A + (-A) =0

Es decir, si sumamos una matriz más la misma matriz pero con todos sus elementos cambiados de signo, el resultado será una matriz nula:

\displaystyle \begin{pmatrix} 4 & 1 & -3 \\[1.1ex] 2 & 0 & 9 \end{pmatrix} + \begin{pmatrix} -4 & -1 & 3 \\[1.1ex] -2 & 0 & -9 \end{pmatrix} = \begin{pmatrix} \bm{0} & \bm{0} & \bm{0} \\[1.1ex] \bm{0} & \bm{0} & \bm{0} \end{pmatrix}

 
  • La suma de matrices también tiene la propiedad del elemento neutro:

\displaystyle A + 0 =A

Esta propiedad es la más evidente, se refiere a que cualquier matriz más una matriz llena de ceros es equivalente a la misma matriz:

\displaystyle \begin{pmatrix} 2 & 1 & 5 \\[1.1ex] -3 & 4 & 9 \\[1.1ex] 1 & 12 & 6 \end{pmatrix} + \begin{pmatrix} 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \end{pmatrix} = \begin{pmatrix} \bm{2} & \bm{1} & \bm{5} \\[1.1ex] \bm{-3} & \bm{4} & \bm{9} \\[1.1ex] \bm{1} & \bm{12} & \bm{6} \end{pmatrix}

 
  • La suma de matrices tiene la propiedad asociativa:

\displaystyle\left( A + B \right) + C =A + \left( B + C \right)

Por lo tanto, es igual el orden en el que sumemos las matrices. Fíjate en el siguiente ejemplo, donde sumamos 3 matrices con un orden diferente y el resultado es el mismo:

\displaystyle A = \begin{pmatrix} 2 \\[1.1ex] 1 \end{pmatrix} \qquad B = \begin{pmatrix} 4 \\[1.1ex] -1 \end{pmatrix} \qquad C = \begin{pmatrix} 3 \\[1.1ex] 0 \end{pmatrix}

\begin{aligned}\left( A + B \right) + C & =\left( \begin{pmatrix} 2 \\[1.1ex] 1 \end{pmatrix} + \begin{pmatrix} 4 \\[1.1ex] -1 \end{pmatrix} \right) + \begin{pmatrix} 3 \\[1.1ex] 0 \end{pmatrix} \\[2ex] & = \begin{pmatrix} 6 \\[1.1ex] 0 \end{pmatrix} + \begin{pmatrix} 3 \\[1.1ex] 0 \end{pmatrix} \\[2ex] & =\begin{pmatrix} \bm{9} \\[1.1ex] \bm{0} \end{pmatrix} \end{aligned}

\begin{aligned} A + \left( B + C \right) & = \begin{pmatrix} 2 \\[1.1ex] 1 \end{pmatrix} + \left( \begin{pmatrix} 4 \\[1.1ex] -1 \end{pmatrix} +\begin{pmatrix} 3 \\[1.1ex] 0 \end{pmatrix} \right) \\[2ex] & = \begin{pmatrix} 2 \\[1.1ex] 1 \end{pmatrix} + \begin{pmatrix} 7 \\[1.1ex] -1 \end{pmatrix} \\[2ex] & = \begin{pmatrix} \bm{9} \\[1.1ex] \bm{0}\end{pmatrix} \end{aligned}

Deja un comentario

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *

Ir arriba