En esta página veremos cómo multiplicar un número por una matriz. Además tienes ejemplos que te ayudarán a entenderlo perfectamente y ejercicios resueltos para que puedas practicar. También encontrarás todas las propiedades del producto de un escalar por una matriz.
¿Cómo hacer una multiplicación de un número por una matriz?
Para multiplicar un número por una matriz, se multiplica cada elemento de la matriz por el número.
Ejemplo:

Ejercicios resueltos de multiplicación de un número por una matriz
Ejercicio 1:
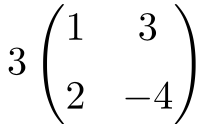
Se trata de una multiplicación de un escalar por una matriz cuadrada de orden 2:
Ejercicio 2:
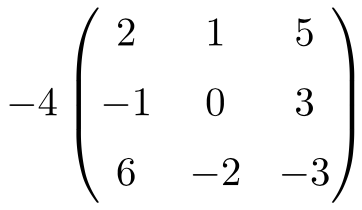
Se trata de un producto de un número por una matriz cuadrada de orden 3:
Ejercicio 3:
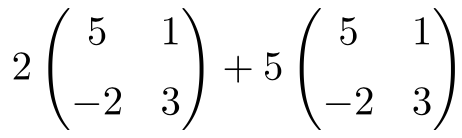
Se trata de una operación que combina productos de números por matrices y sumas de matrices de dimensión 2×2:
Por tanto, primero debemos resolver los productos:
Y finalmente hacemos la suma de las matrices resultantes:
Ejercicio 4:
Dadas las siguientes matrices:
Calcula:
Se trata de una operación que combina multiplicaciones escalares junto con sumas y restas de matrices de dimensión 3×3. Además, la matriz es la matriz identidad, la cual está compuesta por 1 en la diagonal principal y 0 el resto de elementos:
Por tanto, primero hacemos las multiplicaciones:
Sumamos las dos primeras matrices:
Por último, realizamos la resta de las matrices:
Si te han sido útiles estos ejercicios de productos escalares matriciales, no dudes en practicar con los ejercicios resueltos paso a paso de la suma de matrices y del producto de matrices, los dos tipos de operaciones de matrices que más se repiten.
Propiedades del producto de un número por una matriz
Como bien sabes, existen muchos tipos de matrices: matrices cuadradas, matrices triangulares, la matriz identidad,… Pero, por suerte, todas las propiedades del producto de números por matrices sirven para todas las clases de matrices.
Así pues, estas son las propiedades de la multiplicación entre escalares y matrices:
- Propiedad asociativa:
Fíjate en las dos siguientes operaciones como dan el mismo resultado, independientemente de como multipliquemos el 2 y el 3:
- Propiedad distributiva respecto a la suma de escalares:
Como puedes ver en el ejemplo de abajo, es igual si primero sumamos 1+2 y luego lo multiplicamos por una matriz, o si multiplicamos la matriz por separado por 1 y por 2 y después sumamos los resultados:
- Propiedad distributiva respecto a la suma de matrices:
Es decir, sumar dos matrices matemáticas y luego multiplicarlas por un número es equivalente a multiplicar por separado las dos matrices por el mismo número y después sumar los resultados. En el ejemplo de abajo se puede comprobar:
- Propiedad del elemento neutro:
Por lo tanto, al multiplicar una matriz por 1 no modificamos la matriz:
Estas son todas las propiedades del producto de un escalar por una matriz, así que aquí termina este artículo. Esperamos que te haya gustado y, sobre todo, que hayas aprendido a resolver multiplicaciones de números con matrices.
Por otro lado, otras operaciones de matrices relacionadas con la multiplicación, y que son muy útiles, son las potencias. Aquí te dejamos la página donde aprenderás qué es y cómo resolver la potencia de una matriz, por si te entra la curiosidad.


Ideas claras…no tiene pérdida….Magnífico
¡Muchas gracias de nuevo, Juan! 😉
¡Intentamos hacerlo lo mejor posible!
Tengo una presunta con respecto a los ejercicios todos tiene un número entero empezando tipo el primero tiene al principio un 3 el segundo ejercicio un -4, pero que pasaría si en ves de un entero tiene una fracción tipo 2/3 que debería hacer yo ??
Hola José,
Una fracción es, en realidad, un número decimal. Por lo tanto, en tal caso simplemente debes aplicar el mismo procedimiento, de modo que debes multiplicar cada número de la matriz por la fracción.