Potencias de matrices

En esta página veremos cómo hacer potencias de matrices. Además encontrarás ejemplos y ejercicios resueltos paso a paso de potencias de matrices que te ayudarán a entenderlo perfectamente. También aprenderás qué es la potencia n-ésima de una matriz y cómo hallarla.

Sumario
1. ¿Cómo se calcula la potencia de una matriz?
1.1. Ejemplo de cómo calcular la potencia de una matriz:
2. ¿Qué es la potencia n-ésima de una matriz?
2.1. Ejemplo de cómo calcular la potencia n-ésima de una matriz:
3. Ejercicios resueltos de potencias de matrices
3.1. Ejercicio 1
3.2. Ejercicio 2
3.3. Ejercicio 3
3.4. Ejercicio 4
3.5. Ejercicio 5

¿Cómo se calcula la potencia de una matriz?

Para calcular la potencia de una matriz, debemos multiplicar la matriz por ella misma tantas veces como diga el exponente. Por ejemplo:

A^4 = A \cdot A \cdot A \cdot A

Por lo tanto, para poder sacar la potencia de una matriz, debes saber cómo resolver una multiplicación de matrices. De lo contrario, no puedes calcular una potencia matricial.

Ejemplo de cómo calcular la potencia de una matriz:

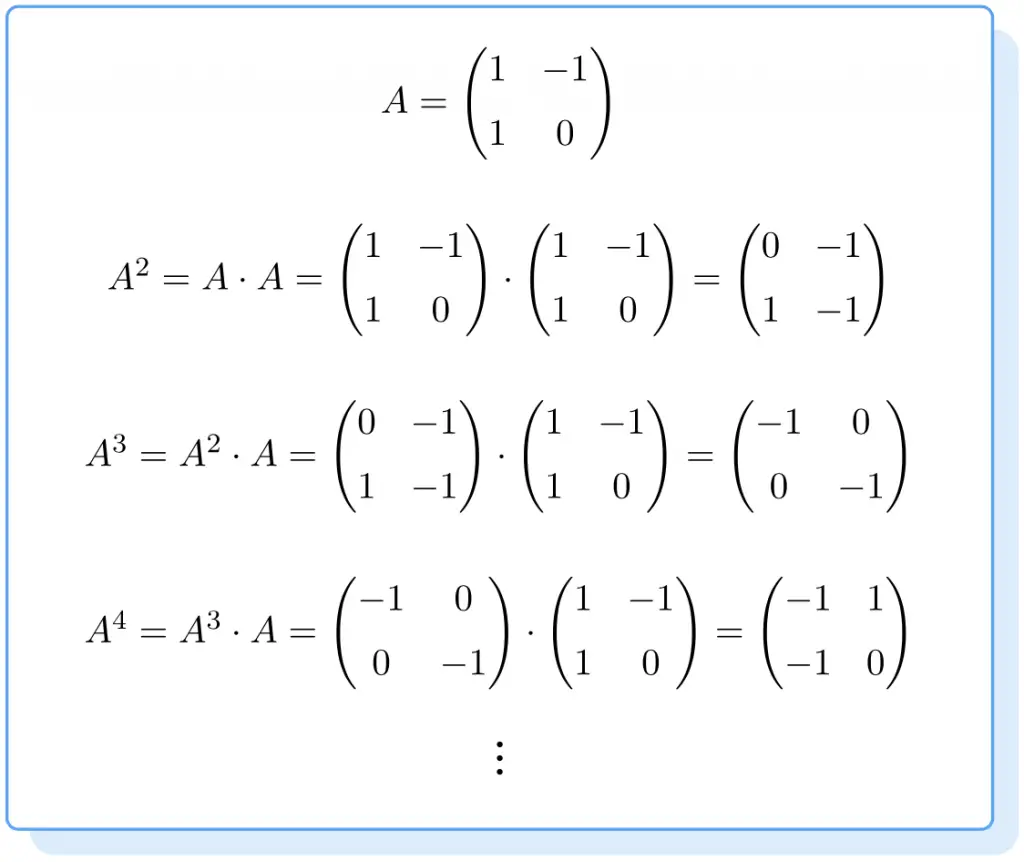
ejemplos de potencias de matrices 2x2

Por lo tanto, la potencia de una matriz elevada al cuadrado se calcula multiplicando la matriz por ella misma. Asimismo, una matriz elevada al cubo es igual a la matriz al cuadrado por la propia matriz. Del mismo modo, para hallar la potencia de una matriz elevada a la cuatro se debe multiplicar la matriz elevada a la tres por la propia matriz. Y así sucesivamente.

Hay una propiedad importante de la potenciación de matrices que debes saber: solo se puede calcular la potencia de una matriz cuando esta es cuadrada, es decir, cuando tiene el mismo número de filas que de columnas.

¿Qué es la potencia n-ésima de una matriz?

La potencia n-ésima de una matriz es una expresión que nos permite calcular cualquier potencia de una matriz fácilmente.

Muchas veces las potencias de matrices siguen un patrón. Por tanto, si conseguimos descifrar la secuencia que siguen, podremos calcular cualquier potencia sin tener que hacer todas las multiplicaciones.

Esto significa que podemos encontrar una fórmula que nos proporcione la potencia enésima de una matriz sin necesidad de calcular todas las potencias.

Trucos para averiguar el patrón que siguen las potencias:

  • La paridad del exponente. Puede ser que las potencias pares sean de una forma y las impares de otra.
  • Variación en los signos. Por ejemplo, podría ser que los elementos de las potencias pares fueran positivos y los elementos de las potencias impares negativos, o viceversa.
  • Repetición: si se repite la misma matriz cada un cierto número de potencias o no.
  • También debemos fijarnos en si hay alguna relación entre el exponente y los elementos de la matriz.

Ejemplo de cómo calcular la potencia n-ésima de una matriz:

  • Siendo A la siguiente matriz, calcula A^n y A^{100} .

\displaystyle A = \begin{pmatrix} 1 & 1 \\[1.1ex] 1 & 1 \end{pmatrix}

Primero vamos a calcular varias potencias de la matriz A , para intentar adivinar el patrón que siguen las potencias. Así que calculamos A^2 , A^3 , A^4 y A^5:

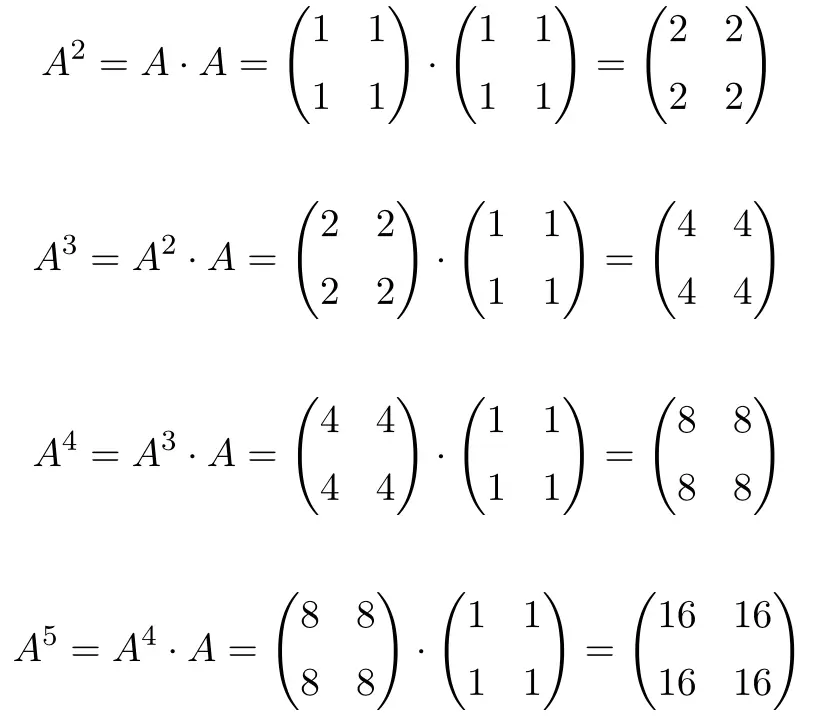
ejercicio resuelto paso a paso de potencias de matrices 2x2

Al calcular hasta A^5 , vemos que las potencias de la matriz A siguen un patrón: a cada aumento de potencia el resultado se multiplica por 2. Por tanto, todas la matrices son potencias de 2:

\displaystyle A^2= \begin{pmatrix} 2 & 2 \\[1.1ex] 2 & 2 \end{pmatrix} =\begin{pmatrix} 2^1 & 2^1 \\[1.1ex] 2^1 & 2^1 \end{pmatrix}

\displaystyle A^3= \begin{pmatrix} 4 & 4 \\[1.1ex] 4 & 4 \end{pmatrix}=\begin{pmatrix} 2^2 & 2^2 \\[1.1ex] 2^2 & 2^2 \end{pmatrix}

\displaystyle A^4= \begin{pmatrix} 8 & 8 \\[1.1ex] 8 & 8 \end{pmatrix}=\begin{pmatrix} 2^3 & 2^3 \\[1.1ex] 2^3 & 2^3 \end{pmatrix}

\displaystyle A^5= \begin{pmatrix} 16 & 16 \\[1.1ex] 16 & 16 \end{pmatrix}=\begin{pmatrix} 2^4 & 2^4 \\[1.1ex] 2^4 & 2^4 \end{pmatrix}

De manera que podemos deducir la fórmula de la potencia n-ésima de la matriz A:

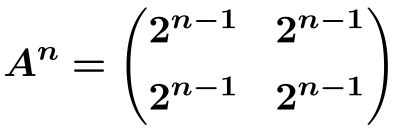
potencia n-esima de una matriz 2x2

Y a partir de esta fórmula podemos calcular A^{100}:

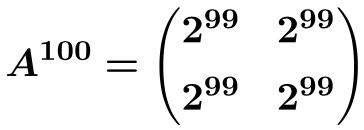
ejercicio resuelto paso a paso de potencia de una matriz 2x2

 

Ejercicios resueltos de potencias de matrices

Ejercicio 1

Dada la siguiente matriz de dimensión 2×2:

\displaystyle A=\begin{pmatrix} 1 & 2 \\[1.1ex] -1 & 1 \end{pmatrix}

Calcula:

\displaystyle A^4

Para calcular la potencia de una matriz, tenemos que ir multiplicando la matriz una por una. Por tanto, primero calculamos \displaystyle A^2 :

\displaystyle A^2= A \cdot A = \begin{pmatrix} 1 & 2 \\[1.1ex] -1 & 1 \end{pmatrix} \cdot \begin{pmatrix} 1 & 2 \\[1.1ex] -1 & 1 \end{pmatrix} = \begin{pmatrix} -1 & 4 \\[1.1ex] -2 & -1\end{pmatrix}

Ahora calculamos \displaystyle A^3 :

\displaystyle A^3= A^2 \cdot A = \begin{pmatrix} -1 & 4 \\[1.1ex] -2 & -1 \end{pmatrix} \cdot \begin{pmatrix} 1 & 2 \\[1.1ex] -1 & 1 \end{pmatrix} =\begin{pmatrix} -5 & 2 \\[1.1ex] -1 & -5 \end{pmatrix}

Y finalmente calculamos \displaystyle A^4 :

\displaystyle A^4= A^3 \cdot A = \begin{pmatrix} -5 & 2 \\[1.1ex] -1 & -5 \end{pmatrix} \cdot \begin{pmatrix} 1 & 2 \\[1.1ex] -1 & 1 \end{pmatrix} = \begin{pmatrix} \bm{-7} & \bm{-8} \\[1.1ex] \bm{4} & \bm{-7} \end{pmatrix}

 

Ejercicio 2

Dada la siguiente matriz de orden 2:

\displaystyle A=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 3 \end{pmatrix}

Calcula:

\displaystyle A^{35}

\displaystyle A^{35} es una potencia demasiado grande para calcularla a mano, por tanto, las potencias de la matriz deben de seguir un patrón. Así que vamos a calcular hasta \displaystyle A^5 para intentar averiguar la secuencia que siguen:

\displaystyle A^2= A \cdot A = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 3 \end{pmatrix} \cdot \begin{pmatrix}1 & 0 \\[1.1ex] 0 & 3 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 9 \end{pmatrix}

\displaystyle A^3= A^2 \cdot A = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 9 \end{pmatrix} \cdot \begin{pmatrix}1 & 0 \\[1.1ex] 0 & 3 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 27 \end{pmatrix}

\displaystyle A^4= A^3 \cdot A = \begin{pmatrix}1 & 0 \\[1.1ex] 0 & 27 \end{pmatrix} \cdot \begin{pmatrix}1 & 0 \\[1.1ex] 0 & 3 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 81 \end{pmatrix}

\displaystyle A^5= A^4 \cdot A = \begin{pmatrix}1 & 0 \\[1.1ex] 0 & 81 \end{pmatrix} \cdot \begin{pmatrix}1 & 0 \\[1.1ex] 0 & 3 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 243 \end{pmatrix}

De esta manera podemos ver el patrón que siguen las potencias: a cada potencia todos los números permanecen igual, excepto el elemento de la segunda columna de la segunda fila, que se multiplica por 3. Por lo tanto, todos los números se quedan siempre igual y el último elemento es una potencia de 3:

\displaystyle A=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 3 \end{pmatrix}=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 3^1 \end{pmatrix}

\displaystyle A^2=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 9 \end{pmatrix}=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 3^2 \end{pmatrix}

\displaystyle A^3=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 27 \end{pmatrix}=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 3^3 \end{pmatrix}

\displaystyle A^4=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 81 \end{pmatrix}=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 3^4 \end{pmatrix}

\displaystyle A^5=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 243 \end{pmatrix}=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 3^5 \end{pmatrix}

Así que la fórmula de la potencia n-ésima de la matriz \displaystyle A es:

\displaystyle A^n=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 3^n\end{pmatrix}

Y a partir de esta fórmula podemos calcular \displaystyle A^{35}:

\displaystyle\bm{A^{35}=}\begin{pmatrix} \bm{1} & \bm{0} \\[1.1ex] \bm{0} & \bm{3^{35}}\end{pmatrix}

 

Ejercicio 3

Dada la siguiente matriz 3×3:

\displaystyle A=\begin{pmatrix} 1 & \frac{1}{5} & \frac{1}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}

Calcula:

\displaystyle A^{100}

\displaystyle A^{100} es una potencia demasiado grande para calcularla a mano, de modo que las potencias de la matriz deben de seguir un patrón. Así que vamos a calcular hasta \displaystyle A^5 para intentar averiguar la secuencia que siguen:

\displaystyle A^2= A \cdot A = \begin{pmatrix} 1 & \frac{1}{5} & \frac{1}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix}1 & \frac{1}{5} & \frac{1}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 1 & \frac{2}{5} & \frac{2}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}

\displaystyle A^3= A^2 \cdot A = \begin{pmatrix} 1 & \frac{2}{5} & \frac{2}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1\end{pmatrix} \cdot \begin{pmatrix}1 & \frac{1}{5} & \frac{1}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 1 & \frac{3}{5} & \frac{3}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}

\displaystyle A^4= A^3 \cdot A = \begin{pmatrix} 1 & \frac{3}{5} & \frac{3}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1\end{pmatrix} \cdot \begin{pmatrix}1 & \frac{1}{5} & \frac{1}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 1 & \frac{4}{5} & \frac{4}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}

\displaystyle A^5= A^4 \cdot A = \begin{pmatrix} 1 & \frac{4}{5} & \frac{4}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1\end{pmatrix} \cdot \begin{pmatrix}1 & \frac{1}{5} & \frac{1}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 1 & \frac{5}{5} & \frac{5}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}

De esta manera podemos ver el patrón que siguen las potencias: a cada potencia todos los números permanecen igual excepto las fracciones, que van aumentando una unidad en el numerador:

\displaystyle A=\begin{pmatrix} 1 & \frac{1}{5} & \frac{1}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}

\displaystyle A^2= \begin{pmatrix} 1 & \frac{2}{5} & \frac{2}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}

\displaystyle A^3= \begin{pmatrix} 1 & \frac{3}{5} & \frac{3}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}

\displaystyle A^4= \begin{pmatrix} 1 & \frac{4}{5} & \frac{4}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}

\displaystyle A^5= \begin{pmatrix} 1 & \frac{5}{5} & \frac{5}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}

Así que la fórmula de la potencia de la matriz enesima \displaystyle A es:

\displaystyle A^n= \begin{pmatrix} 1 & \frac{n}{5} & \frac{n}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}

Y a partir de esta fórmula podemos calcular \displaystyle A^{100}:

\displaystyle A^{100}= \begin{pmatrix} 1 & \frac{100}{5} & \frac{100}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}= \begin{pmatrix} \bm{1} & \bm{20} & \bm{20} \\[1.1ex] \bm{0} & \bm{1} & \bm{0} \\[1.1ex] \bm{0} & \bm{0} & \bm{1} \end{pmatrix}

 

Ejercicio 4

Dada la siguiente matriz de tamaño 2×2:

\displaystyle A=\begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix}

Calcula:

\displaystyle A^{201}

\displaystyle A^{201} es una potencia demasiado grande para calcularla a mano, por tanto, las potencias de la matriz tienen que seguir un patrón. En este caso debemos calcular hasta \displaystyle A^{8}  para poder averiguar la secuencia que siguen:

\displaystyle A^2= A \cdot A = \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} \cdot \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} = \begin{pmatrix} -1 & 0 \\[1.1ex] 0 & -1 \end{pmatrix}

\displaystyle A^3= A^2 \cdot A = \begin{pmatrix} -1 & 0 \\[1.1ex] 0 & -1 \end{pmatrix} \cdot \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} = \begin{pmatrix} 0 & 1 \\[1.1ex] -1 & 0 \end{pmatrix}

\displaystyle A^4= A^3 \cdot A = \begin{pmatrix}0 & 1 \\[1.1ex] -1 & 0 \end{pmatrix} \cdot \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix} = \bm{I}

\displaystyle A^5= A^4 \cdot A = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1\end{pmatrix} \cdot \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} = \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix}

\displaystyle A^6= A^5 \cdot A = \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} \cdot \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} = \begin{pmatrix} -1 & 0 \\[1.1ex] 0 & -1 \end{pmatrix}

\displaystyle A^7= A^6 \cdot A = \begin{pmatrix} -1 & 0 \\[1.1ex] 0 & -1 \end{pmatrix} \cdot \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} = \begin{pmatrix} 0 & 1 \\[1.1ex] -1 & 0 \end{pmatrix}

\displaystyle A^8= A^7 \cdot A = \begin{pmatrix}0 & 1 \\[1.1ex] -1 & 0 \end{pmatrix} \cdot \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix} = \bm{I}

Con estos cálculos podemos ver que cada 4 potencias obtenemos la matriz identidad. Es decir, nos dará como resultado la matriz identidad las potencias \displaystyle A^4, \displaystyle A^8, \displaystyle A^{12}, \displaystyle A^{16},… Así que para calcular \displaystyle A^{201} tenemos que descomponer el 201 en múltiplos de 4:

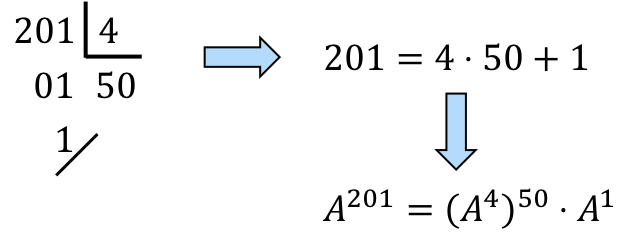
ejercicio resuelto paso a paso de potencias de matrices 2x2 y de potencia n-ésima

\displaystyle 201= 4 \cdot 50 +1 , por tanto, A^{201} será 50 veces \displaystyle A^{4} y una vez \displaystyle A^{1}:

\displaystyle A^{201}=\left(A^4 \right)^{50} \cdot A^1

Y como sabemos que \displaystyle A^4 es la matriz identidad \displaystyle I :

\displaystyle A^4 =I

\displaystyle A^{201}=\left(A^4 \right)^{50} \cdot A^1 = I^{50}\cdot A

A parte, la matriz identidad elevada a cualquier número da la matriz identidad. Por tanto:

\displaystyle A^{201}= I^{50}\cdot A = I \cdot A

Y, por último, cualquier matriz multiplicada por la matriz identidad da como resultado la misma matriz. Por lo tanto:

\displaystyle A^{201}= I \cdot A = A

Por lo que A^{201} es igual a A:

\displaystyle A^{201}= A =\begin{pmatrix} \bm{0} & \bm{-1} \\[1.1ex] \bm{1} & \bm{0} \end{pmatrix}

 

Ejercicio 5

Dada la siguiente matriz de orden 3:

\displaystyle A=\begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & -3 & 1 \\[1.1ex] -2 & -3 & 0 \end{pmatrix}

Calcula:

\displaystyle A^{62}

Evidentemente, calcular la potenciación de la matriz \displaystyle A^{62} resulta un cálculo demasiado grande para hacerlo a mano, por tanto, las potencias de la matriz tienen que seguir un patrón. En este caso debemos calcular hasta \displaystyle A^{6}  para poder averiguar la secuencia que siguen:

\displaystyle A^2= A \cdot A = \begin{pmatrix}3 & 4 & -1 \\[1.1ex] -2 & -3 & 1 \\[1.1ex] -2 & -3 & 0 \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & -3 & 1 \\[1.1ex] -2 & -3 & 0 \end{pmatrix} = \begin{pmatrix} 3 & 3 & 1 \\[1.1ex] -2 & -2 & -1 \\[1.1ex] 0 & 1 & -1 \end{pmatrix}

\displaystyle A^3= A^2 \cdot A = \begin{pmatrix}3 & 3 & 1 \\[1.1ex] -2 & -2 & -1 \\[1.1ex] 0 & 1 & -1\end{pmatrix} \cdot \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & -3 & 1 \\[1.1ex] -2 & -3 & 0 \end{pmatrix} = \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}

\displaystyle A^4= A^3 \cdot A = \begin{pmatrix}1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & -3 & 1 \\[1.1ex] -2 & -3 & 0 \end{pmatrix} = \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & -3 & 1 \\[1.1ex] -2 & -3 & 0 \end{pmatrix}

\displaystyle A^5= A^4 \cdot A = \begin{pmatrix}3 & 4 & -1 \\[1.1ex] -2 & -3 & 1 \\[1.1ex] -2 & -3 & 0 \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & -3 & 1 \\[1.1ex] -2 & -3 & 0 \end{pmatrix} = \begin{pmatrix} 3 & 3 & 1 \\[1.1ex] -2 & -2 & -1 \\[1.1ex] 0 & 1 & -1 \end{pmatrix}

\displaystyle A^6= A^5 \cdot A = \begin{pmatrix}3 & 3 & 1 \\[1.1ex] -2 & -2 & -1 \\[1.1ex] 0 & 1 & -1\end{pmatrix} \cdot \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & -3 & 1 \\[1.1ex] -2 & -3 & 0 \end{pmatrix} = \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}

Con estos cálculos podemos ver que cada 3 potencias obtenemos la matriz identidad. Es decir, nos dará como resultado la matriz identidad las potencias \displaystyle A^3, \displaystyle A^6, \displaystyle A^{9}, \displaystyle A^{12},… De manera que para calcular \displaystyle A^{62} tenemos que descomponer el 62 en múltiplos de 3:

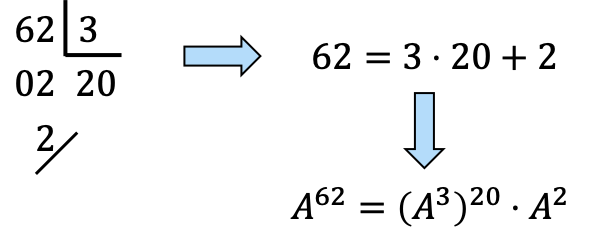
ejercicio resuelto paso a paso de una potencia de una matriz 3x3, potencia enésima

\displaystyle 62= 3 \cdot 20 +2 , por tanto, \displaystyle A^{62} será 20 veces \displaystyle A^{3} y una vez \displaystyle A^{2}:

\displaystyle A^{62}=\left(A^3 \right)^{20} \cdot A^2

Y como sabemos que \displaystyle A^3 es la matriz identidad \displaystyle I :

\displaystyle A^3 =I

\displaystyle A^{62}=\left(A^3 \right)^{20} \cdot A^2 = I^{20}\cdot A^2

A parte, la matriz identidad elevada a cualquier número da la matriz identidad. Por tanto:

\displaystyle A^{62}= I^{20}\cdot A^2 = I \cdot A^2

Finalmente, cualquier matriz multiplicada por la matriz identidad da como resultado la misma matriz. Por tanto:

\displaystyle A^{62}= I \cdot A^2 = A^2

Por lo que A^{62}  será igual a A^{2} , cuyo resultado lo hemos calculado anteriormente:

\displaystyle A^{62}= A^2=\begin{pmatrix} \bm{3} & \bm{3} & \bm{1} \\[1.1ex] \bm{-2} & \bm{-2} & \bm{-1} \\[1.1ex] \bm{0} & \bm{1} & \bm{-1} \end{pmatrix}

 

Si te han sido útiles estos ejercicios de potencias de matrices cuadradas, también puedes encontrar ejercicios resueltos paso a paso de suma y resta de matrices, una de las operaciones con matrices que más se utilizan.

 

Deja un comentario

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *

Ir arriba