¿Qué son dos matrices Semejantes (o Similares)? Ejemplos, Propiedades, etc.

En esta página encontrarás la explicación de las matrices semejantes, también conocidas como matrices similares. Además, te mostramos un ejemplo claro de dos matrices semejantes y todas las propiedades de este tipo de matrices para que no te quede ninguna duda. Por último, incluso podrás ver la relación que tienen con las matrices congruentes.

Sumario

1. ¿Qué son las matrices semejantes (o similares)?

2. Ejemplo de matrices semejantes o similares

3. Propiedades de las matrices semejantes

4. Matrices congruentes

¿Qué son las matrices semejantes (o similares)?

La definición de matrices semejantes es la siguiente:

Dos matrices $A$ y $B$ son semejantes (o similares) si existe una matriz $P$ con la que cumplen la siguiente condición:

$P^{-1}AP = B$

O equivalentemente:

$AP = PB$

En realidad, la matriz $P$ actúa como matriz de cambio de base. Por lo tanto, lo que significa esta ecuación es que la matriz $A$ se puede expresar en otra base ( $P$ ), que da lugar a la matriz $B$ .

También se puede llamar a este término como transformación de semejanza, ya que en realidad estamos transformando la matriz $A$ en la matriz $B$ .

Evidentemente, la matriz $P$ tiene que ser una matriz regular o no degenerada (determinante diferente de cero).

Por otro lado, se puede indicar que dos matrices son semejantes con la siguiente expresión:

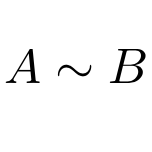
explicacion de las matrices semejantes o similares

Esta clase de matrices es más importante de lo que parece para el álgebra lineal. Se utilizan sobre todo para las matrices diagonalizables, porque el procedimiento para diagonalizar cualquier matriz se basa en el concepto de semejanza de matrices.

De hecho, el proceso de la diagonalización de una matriz consiste en calcular una matriz semejante que, a la vez, es una matriz diagonal. Puedes ver cómo se hace en cómo diagonalizar una matriz.

Ejemplo de matrices semejantes o similares

A continuación veremos un ejemplo de matrices semejantes de dimensión 2×2 para acabar de asimilar concepto.

Las matrices cuadradas A y B son semejantes entre ellas a través de la matriz invertible P:

$\displaystyle A= \begin{pmatrix}-1&2\\[1.1ex] 3&1\end{pmatrix} \qquad B= \begin{pmatrix}-5&-3\\[1.1ex] 6&5\end{pmatrix}$

$\displaystyle P= \begin{pmatrix}2&1\\[1.1ex] -1&0\end{pmatrix}$

Para demostrar que se trata de matrices semejantes entre sí, primero debemos calcular la matriz inversa de P:

$\displaystyle P^{-1}= \begin{pmatrix}0&-1\\[1.1ex] 1&2\end{pmatrix}$

Y ahora comprobamos que son semejantes realizando el producto matricial que define la similitud de dos matrices:

$\displaystyle P^{-1}AP = B \quad ?$

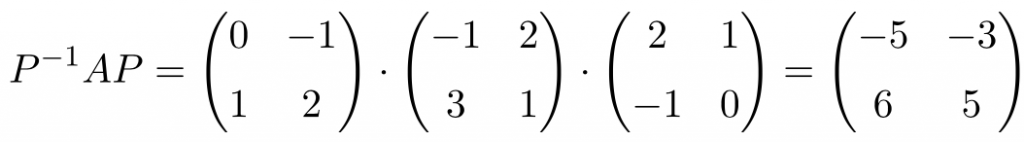
ejemplos de matrices semejantes o similares 2x2

$\displaystyle P^{-1}AP = B$ ✅

Sí que se cumple la relación de semejanza, por lo que son matrices semejantes.

Propiedades de las matrices semejantes

Dos matrices A y B que son semejantes comparten las siguientes características:

Mismo rango.

$rg(A)=rg(B)$

Los determinantes de ambas matrices son iguales.

$det(A)=det(B)$

Misma traza.

$tr(A)=tr(B)$

Mismos autovalores (o valores propios). Sin embargo, los vectores propios (o autovectores) son distintos generalmente.

Mismo polinomio característico y polinomio mínimo.

La transpuesta de una matriz es semejante con la matriz original.

Se puede hallar la matriz B aplicando operaciones elementales en las filas de la matriz A, y viceversa.

Evidentemente, la semejanza es reflexiva. Es decir, si A es semejante a B, B también es semejante a A.

Además, la similaridad de matrices también es simétrica. O dicho de otra forma, si con la matriz P se puede obtener la matriz que es semejante a A (B), también se puede obtener la matriz que es semejante a B (A) con la misma matriz P:

$B=P^{-1}AP$

$A=PBP^{-1}$

Asimismo, la semejanza es transitiva. De manera que si la matriz A es semejante con la matriz B, y esta es semejante con la matriz C, la matriz A también es semejante con la matriz C.

$\left. \begin{array}{l}A\sim B \\[2ex] B \sim C \end{array}\right\} \longrightarrow A \sim C$

Finalmente, toda matriz es semejante con una matriz escalonada. Y de este propiedad se puede deducir el siguiente corolario: toda matriz cuadrada es semejante con una matriz triangular.

Matrices congruentes

Por otra parte, también existe otra relación entre matrices muy parecida pero en vez de ser con la matriz inversa es con la matriz traspuesta. Se llama congruencia.

Dos matrices A y B son congruentes si existe una matriz invertible P con la que se cumple la siguiente igualdad:

$P^tAP = B$

Como puedes ver, es el análogo de las matrices semejantes pero con la matriz transpuesta.

Matrices semejantes o similares

¿Qué son las matrices semejantes (o similares)?

Ejemplo de matrices semejantes o similares

Propiedades de las matrices semejantes

Matrices congruentes

Deja un comentario Cancelar respuesta