Matrices complejas: matriz conjugada y traspuesta conjugada

En esta página verás que son las matrices complejas, las matrices conjugadas y las matrices traspuestas conjugadas. Ahora te suenan muy iguales, pero ya verás como al final de la página entenderás perfectamente la diferencia entre cada una. Además, veremos ejemplos de cada tipo y sus propiedades.

Sumario

1. Matriz compleja

1.1. ¿Qué es una matriz compleja?

1.2. Ejemplos de matrices complejas

2. Matriz conjugada

2.1. ¿Qué es una matriz conjugada?

2.2. Ejemplo de matriz conjugada

2.3. Propiedades de la matriz conjugada

3. Matriz traspuesta conjugada

3.1. ¿Qué es una matriz traspuesta (o transpuesta) conjugada?

3.2. Ejemplo de matriz traspuesta conjugada

3.3. Propiedades de la matriz traspuesta conjugada

Matriz compleja

Antes de ver la explicación de la matriz conjugada y de la matriz conjugada traspuesta, vamos a repasar el concepto de matriz compleja:

¿Qué es una matriz compleja?

Una matriz compleja es una matriz que tiene algún número complejo entre sus elementos.

Recuerda que un número complejo o imaginario es un número formado por una parte real y otra parte imaginaria, la cual se indica con la letra i. Por ejemplo:

$3+5i$

Ejemplos de matrices complejas

Veamos algunos ejemplos de matrices complejas de varias dimensiones:

Ejemplo de matriz compleja de orden 2×2

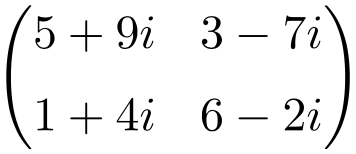
Ejemplo de matriz compleja de dimensión 3×3

Ejemplo de matriz compleja de tamaño 4×4

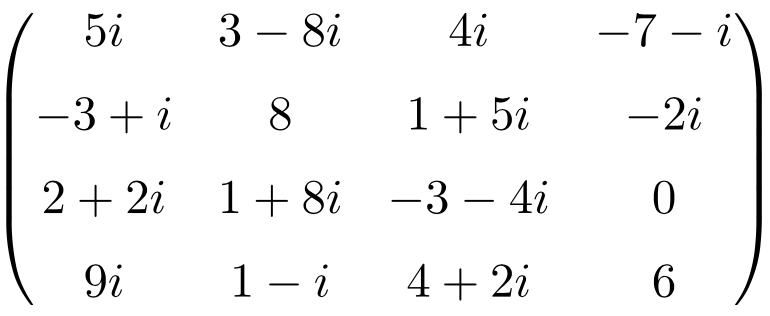
Matriz conjugada

Una vez vista cuál es la definición de matriz compleja, veamos qué son una matriz conjugada y una matriz conjugada traspuesta:

¿Qué es una matriz conjugada?

Una matriz conjugada es una matriz compleja a la que se han sustituido todos sus elementos por sus conjugados, es decir, se ha cambiado el signo de la parte imaginaria de todos sus números complejos.

La matriz conjugada de $A$ se expresa con una barra horizontal encima: $\overline{A}$ .

Ejemplo de matriz conjugada

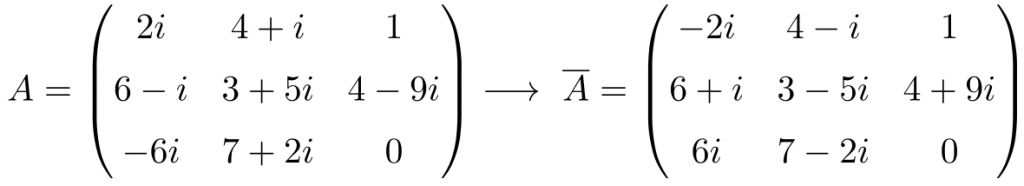
Propiedades de la matriz conjugada

Las características de este tipo de matriz son las siguientes:

La conjugada de una matriz conjugada es la matriz original.

$\displaystyle \overline{\bigl( \ \overline{A} \vphantom{A^{9^1}} \ \bigr)} = A$

Sumar (o restar) dos matrices y conjugar el resultado es lo mismo que primero conjugar las dos matrices por separado y luego sumarlas (o restarlas).

$\displaystyle \overline{\bigl( A \pm B \bigr)} = \overline{A} \pm \overline{B}$

El producto conjugado de dos matrices es igual a conjugar las dos matrices por separado y después calcular la multiplicación matricial.

$\displaystyle \overline{\bigl( A \cdot B \bigr)} = \overline{A} \cdot \overline{B}$

Multiplicar una matriz por un escalar y conjugar el resultado da lo mismo que primero hacer los conjugados del escalar y la matriz y luego resolver el producto.

$\displaystyle \overline{\bigl( k \cdot A \bigr)} = \overline{k} \cdot \overline{A}$

Trasponer una matriz y luego conjugarla es lo mismo que primero conjugar la matriz y luego hacer su trasposción.

$\displaystyle \overline{\bigl(A^t \bigr)} = \left( \overline{A}\right)^t$

Hacer la inversa de una matriz y después conjugarla es idéntico a conjugar la matriz y más tarde invertirla.

$\displaystyle \overline{\bigl( A^{-1} \bigr)} = \left(\overline{A} \right)^{-1}$

El rango de una matriz conjugada es igual al rango de la misma matriz sin conjugar.

$\displaystyle rg\left(\overline{A}\right) =rg(A)$

Es indiferente calcular la traza de una matriz conjugada o calcular la traza de la misma matriz sin conjugar y después hacer la conjugación del resultado.

$\displaystyle tr\left(\overline{A}\right) =\overline{tr(A)}$

Por último, sacar el determinante de una matriz conjugada es igual a calcular el conjugado del resultado del determinante de la misma matriz sin conjugar.

$\displaystyle det\left(\overline{A}\right) = \overline{det(A)}$

Matriz traspuesta conjugada

Finalmente, después de ver cómo conjugar una matriz, pasamos al concepto de matriz traspuesta conjugada:

¿Qué es una matriz traspuesta (o transpuesta) conjugada?

La matriz traspuesta (o transpuesta) conjugada es la que se obtiene después de trasponer una matriz y luego hacer su conjugada.

Este tipo de matriz también se le llama matriz adjunta o simplemente adjunta de una matriz. Además, se suele representar con un asterisco $(A^*)$ , aunque hay algunos matemáticos que la dibujan como $A^*$ o $A^H$ .

Ejemplo de matriz traspuesta conjugada

A continuación tienes un ejemplo de cómo calcular la traspuesta (o transpuesta) conjugada de una matriz:

$\displaystyle A=\begin{pmatrix}1+3i&2-i & -4i \\[1.1ex] 6 & 8+2i & 3-5i \\[1.1ex] 7i & 1+9i & -2+i\end{pmatrix}$

En primer lugar, hacemos la transposición de la matriz A:

$\displaystyle A^t=\begin{pmatrix}1+3i& 6 & 7i \\[1.1ex] 2-i & 8+2i & 1+9i \\[1.1ex] -4i & 3-5i & -2+i\end{pmatrix}$

Y luego calculamos la matriz conjugada de la traspuesta, o dicho de otra forma, cambiamos el signo de la parte imaginaria de todos los números complejos:

$\displaystyle A^*=\overline{A^t}=\begin{pmatrix}1-3i& 6 & -7i \\[1.1ex] 2+i & 8-2i & 1-9i \\[1.1ex] 4i & 3+5i & -2-i\end{pmatrix}$

Por lo tanto, el resumen del cálculo de la matriz traspuesta conjugada es:

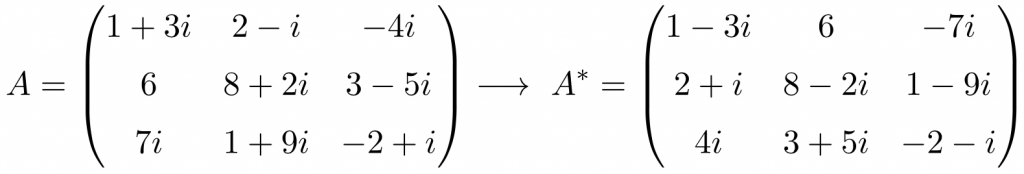
matriz traspuesta conjugada de dimension 3x3

Propiedades de la matriz traspuesta conjugada

Las propiedades de este tipo de matriz cuadrada son las siguientes:

La matriz traspuesta conjugada de una matriz anteriormente ya transpuesta y conjugada es la matriz original.

$\displaystyle \bigl(A^*\bigr) ^* = A$

La propiedad de adición de matrices traspuestas conjugadas dice que hacer la suma (o la resta) de dos matrices y luego aplicar al resultado esta operación es lo mismo que primero hacer la traspuesta conjugada de cada matriz y luego sumar (o restar) los resultados.

$\displaystyle \bigl( A\pm B \bigr)^* = A^*\pm B^*$

Multiplicar dos matrices y luego hacer su traspuesta conjugada da el mismo resultado que el producto inverso de las matrices traspuestas conjugadas.

$\displaystyle \bigl( A\cdot B \bigr)^* = B^*\cdot A^*$

Calcular la matriz traspuesta conjugada del producto de un escalar por una matriz es idéntico a conjugar el número complejo y hallar la traspuesta conjugada de la matriz por separado y luego hacer la multiplicación.

$\displaystyle \bigl( k\cdot A \bigr)^* = \overline{k}\cdot A^*$

Si la matriz es invertible, es indiferente el orden en el que se hagan las operaciones inversa de la matriz y traspuesta de la conjugada.

$\displaystyle \bigl( A^{-1} \bigr)^*= \bigl( A^* \bigr)^{-1}$

2 comentarios en “Matriz Compleja, Conjugada y Traspuesta conjugada”

Juan
30/12/2021 a las 17:41

Esta genial todo el articulo, muy bien explicado y con excelente contenido, muy completo!!

Responder
1. Matrices y Determinantes
  31/12/2021 a las 10:42
  
  ¡Muchísimas gracias Juan!
  
  Responder