Matriz Identidad (o Unidad): definición, ejemplos, propiedades, etc.

En esta página verás qué es la matriz Identidad (o Unidad) junto con varios ejemplos. Además, explicamos cuáles son las propiedades de la matriz Identidad, cómo operar con este tipo de matriz y cuál es el resultado de su determinante. Finalmente, encontrarás las aplicaciones que tiene esta matriz tan especial.

Sumario

1. ¿Qué es la matriz Identidad?

2. Ejemplos de matrices Identidades

3. Propiedades de la matriz Identidad

4. Operaciones con la matriz Identidad (o Unidad)

4.1. Suma y resta con la matriz Identidad

4.2. Multiplicación de una matriz por la matriz Identidad

4.3. Potencia de la matriz Identidad

5. Determinante de la matriz Identidad

6. Aplicaciones de la matriz Identidad

¿Qué es la matriz Identidad?

La matriz Identidad (o Unidad) es una matriz cuadrada llena de ceros (0) excepto en la diagonal principal, donde todos los elementos son unos (1).

Esta es la definición de la matriz Identidad o matriz Unidad, pero seguro que lo ves más claro mediante ejemplos:

Ejemplos de matrices Identidades

Ejemplo de matriz Identidad de dimensión 2×2

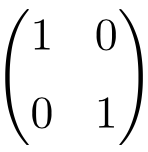
matriz identidad o unica de dimension 2x2

Ejemplo de matriz Identidad de orden 3×3

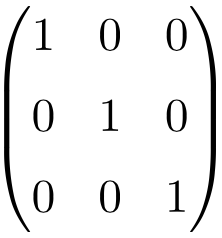
matriz identidad o unica de dimension 3x3

Ejemplo de matriz Identidad de tamaño 4×4

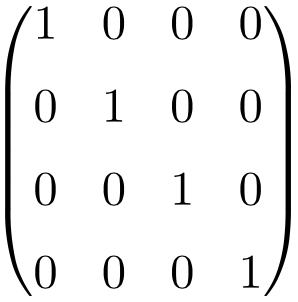
matriz identidad o unica de dimension 4x4

Como puedes ver, para construir la matriz Identidad siempre tenemos que hacer el mismo procedimiento: poner unos (1) en la diagonal principal y el resto todo ceros (0). Lo único que cambia es la dimensión de la matriz.

Propiedades de la matriz Identidad

La matriz Identidad, matriz Unidad o incluso matriz Idéntica es muy utilizada en las matemáticas, y eso es debido a las características que tiene este tipo de matriz:

La matriz Identidad es un ejemplo de matriz diagonal.

Una matriz Unidad es una matriz triangular superior e inferior a la vez.

La matriz Identidad también es una matriz simétrica.

La adjunta de la matriz Identidad es ella misma.

$\displaystyle \text{Adj}(I) =\begin{pmatrix} 1&0&0\\[1.1ex] 0&1&0 \\[1.1ex] 0&0&1 \end{pmatrix}$

Es una matriz invertible. Y, al igual que con la adjunta, la inversa de la matriz Unidad es ella misma:

$\displaystyle I^{-1}=\begin{pmatrix} 1&0&0\\[1.1ex] 0&1&0 \\[1.1ex] 0&0&1 \end{pmatrix}$

Cualquier matriz escalar se puede obtener a partir de la multiplicación de un número por la matriz Identidad:

$\displaystyle 3\cdot \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 3 & 0 & 0 \\[1.1ex] 0 & 3 & 0 \\[1.1ex] 0 & 0 & 3 \end{pmatrix}$

Todos valores propios (o autovalores) de la matriz Idéntica son 1:

$\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} \longrightarrow \ \lambda = 1 \ ; \ \lambda = 1 \ ; \ \lambda = 1$

Por último, la matriz Identidad también es un ejemplo de matriz permutación.

Operaciones con la matriz Identidad (o Unidad)

Seguro que estás pensando: todo esto está muy bien pero… ¿y para qué sirve la matriz Identidad? ¡Si tan solo es una matriz con ceros y unos!

Aunque quizá aún no hayas dado ese temario, la matriz Identidad se utiliza mucho en las matemáticas, de hecho, este tipo de matriz cuadrada tiene mucha importancia en álgebra lineal. La principal utilidad de la matriz Identidad es la facilidad con la que permite realizar cálculos de operaciones matriciales. Veamos pues cómo operar con la matriz Identidad:

Suma y resta con la matriz Identidad

Una manera de sumar (o restar) números en la diagonal principal de una matriz sin modificar los otros elementos es a través de la matriz Identidad, ya que solamente suma (o resta) una unidad a esos elementos:

$\displaystyle \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & 0 & 5 \\[1.1ex] 9 & 6 & -7 \end{pmatrix}+\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 4 & 4 & -1 \\[1.1ex] -2 & 1 & 5 \\[1.1ex] 9 & 6 & -6 \end{pmatrix}$

$\displaystyle \begin{pmatrix} 1 & 7 & 4 \\[1.1ex] 8 & -2 & 3 \\[1.1ex] 0 & 5 & 9 \end{pmatrix}-\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 0 & 7 & 4 \\[1.1ex] 8 & -3 & 3 \\[1.1ex] 0 & 5 & 8 \end{pmatrix}$

También se pueden sumar o restar más unidades a los elementos de la diagonal multiplicando primero la matriz Identidad por un escalar:

$\displaystyle \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & 0 & 5 \\[1.1ex] 9 & 6 & -7 \end{pmatrix}+5\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 8 & 4 & -1 \\[1.1ex] -2 & 5 & 5 \\[1.1ex] 9 & 6 & -2 \end{pmatrix}$

$\displaystyle \begin{pmatrix} 1 & 7 & 4 \\[1.1ex] 8 & -2 & 3 \\[1.1ex] 0 & 5 & 9 \end{pmatrix}-4\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} -3 & 7 & 4 \\[1.1ex] 8 & -6 & 3 \\[1.1ex] 0 & 5 & 5 \end{pmatrix}$

Multiplicación de una matriz por la matriz Identidad

Al multiplicar cualquier matriz por la matriz Identidad, esta actúa como elemento neutro, es decir, cualquier matriz multiplicada por la matriz Identidad da como resultado la misma matriz. Fíjate en el siguiente ejemplo:

$\displaystyle \begin{pmatrix} -3 & 1 & 0 \\[1.1ex] 5 & 2 & -4 \\[1.1ex] 1 & 0 & 6 \end{pmatrix}\cdot \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} -3 & 1 & 0 \\[1.1ex] 5 & 2 & -4 \\[1.1ex] 1 & 0 & 6 \end{pmatrix}$

Además, el sentido del producto matricial es indiferente, o dicho de otra forma, da igual si multiplicamos la matriz Identidad por la derecha o por izquierda que el resultado siempre será la misma matriz. Para demostrarlo, a continuación repetimos el ejercicio anterior pero esta vez multiplicando la matriz Identidad por el lado opuesto:

$\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}\cdot \displaystyle \begin{pmatrix} -3 & 1 & 0 \\[1.1ex] 5 & 2 & -4 \\[1.1ex] 1 & 0 & 6 \end{pmatrix} = \begin{pmatrix} -3 & 1 & 0 \\[1.1ex] 5 & 2 & -4 \\[1.1ex] 1 & 0 & 6 \end{pmatrix}$

Potencia de la matriz Identidad

La potencia de la matriz Identidad siempre da como resultado la matriz Identidad, independientemente del exponente al que elevemos la matriz y de la dimensión de esta.

$\left.\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}\right. ^2 =\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

$\left.\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}\right. ^3 =\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}$

$\left.\begin{pmatrix} 1 & 0 & 0 & 0\\[1.1ex] 0 & 1 & 0 & 0\\[1.1ex] 0 & 0 & 1 & 0 \\[1.1ex] 0& 0 &0&1\end{pmatrix}\right. ^5 =\begin{pmatrix} 1 & 0 & 0 & 0\\[1.1ex] 0 & 1 & 0 & 0\\[1.1ex] 0 & 0 & 1 & 0 \\[1.1ex] 0& 0 &0&1\end{pmatrix}$

$\left.\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}\right. ^n =\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

Determinante de la matriz Identidad

Como supongo que ya te estarás imaginando, el determinante de la matriz Identidad (o Unidad) siempre es igual a 1, indistintamente de la dimensión de la matriz.

$\displaystyle\begin{vmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{vmatrix} = \bm{1}$

$\displaystyle\begin{vmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{vmatrix}=\bm{1}$

$\displaystyle\begin{vmatrix} 1 & 0 & 0 & 0 \\[1.1ex] 0 & 1 & 0 & 0 \\[1.1ex] 0 & 0 & 1 & 0 \\[1.1ex] 0 & 0 & 0 & 1 \end{vmatrix}=\bm{1}$

Aplicaciones de la matriz Identidad

Finalmente, después de toda esta información, seguro que ya sabes responder a la típica pregunta de ¿por qué es tan importante la matriz Identidad? Tranqui, yo también me hacía esta pregunta antes. 😂

Como habrás observado, la matriz Identidad tiene muchas utilidades y por eso tiene tanto interés. Una de las utilidades de la matriz Unidad son las operaciones, ya que, como hemos visto, es muy fácil realizar operaciones matriciales con ella.

Por otro lado, la matriz Identidad también se utiliza para resolver ecuaciones matriciales. Para ello se aprovecha la siguiente propiedad de matriz inversa: la multiplicación de una matriz por su matriz invertida es igual a la matriz Identidad. Puedes ver cómo se soluciona una ecuación con matrices haciendo click en el link.

Además, la matriz Identidad también se usa para calcular la matriz inversa con el método de Gauss. Este método se basa en colocar una matriz al lado de la matriz Identidad, formando así una matriz más grande. Luego se tiene que ir transformando la matriz original en la matriz Identidad aplicando operaciones elementales en las filas. Parece muy complicado pero en realidad no lo es tanto, sin embargo se tiene que aplicar todo un procedimiento, así que si estás más interesad@ puedes buscar cómo se invierte una matriz en el buscador de la página web (arriba a la derecha).

Por último, la matriz Identidad también es útil para diagonalizar una matriz y calcular sus valores propios (o autovalores). Porque mediante unas operaciones, en las que interviene la matriz Unidad, se puede conseguir el polinomio característico del cual se obtienen los valores propios. Pero esto ya es un temario muy avanzado, por eso tenemos toda una página súper extensa dedicada a la diagonalización de matrices con ejemplos y ejercicios resueltos explicándolo. Si estás más interesad@ puedes buscar esta guía en nuestro buscador (arriba a la derecha).

4 comentarios en “Matriz Identidad o Unidad”

Ruth Quero
03/12/2021 a las 18:53

Estó ayudo a resolver mis dudas y problemas.😊😊😊

Responder
1. Matrices y Determinantes
  04/12/2021 a las 14:14
  
  ¡Me alegro de que te sirva Ruth! Cualquier duda también puedes preguntarla en los comentarios.
  
  Responder
Aroa
02/06/2022 a las 09:15

Hola! Tendría una duda. Hay veces que la matriz identidad aparece como «I» sin indicar con ningún número su orden. ¿Cómo podríamos saber cuál es?
Gracias.

Responder
1. Matrices y Determinantes
  02/06/2022 a las 23:38
  
  Hola Arola,
  
  En tal caso, la matriz identidad es del orden necesario. Por ejemplo, solo se pueden sumar y restar matrices con las mismas dimensiones, por lo tanto, si estás haciendo una suma de matrices 2×2 la matriz identidad también será 2×2.
  
  Responder