¿Qué es una matriz Involutiva? (Ejemplos y Propiedades) ✅

En esta página aprenderás qué es una matriz involutiva. Además te enseñamos ejemplos de matrices involutivas de dimensión 2×2, 3×3 y 4×4. Y, por último, encontrarás la fórmula de una matriz involutiva.

Sumario

1. ¿Qué es una matriz involutiva?

2. Ejemplos de matrices involutivas

2.1. Ejemplo de matriz involutiva 2×2:

2.2. Ejemplo de matriz involutiva 3×3:

2.3. Ejemplo de matriz involutiva 4×4:

3. Fórmula de la matriz involutiva

4. Propiedades de una matriz involutiva

¿Qué es una matriz involutiva?

El significado de matriz involutiva es el siguiente:

Definición de matriz involutiva: una matriz cuadrada e invertible cuya matriz inversa es la propia matriz.

$A^{-1} = A$

Donde $A$ es una matriz cualquiera y $A^{-1}$ representa su inversa.

Así que, evidentemente, una matriz involutiva es un ejemplo de matriz regular o no degenerada.

Si no sabes qué es la inversa de una matriz, aquí puedes ver cómo calcular la matriz inversa 3×3. Es importante saber invertir una matriz, sin embargo, para ello también se necesita saber cómo se calcula el adjunto de una matriz.

Pero volvamos al tema: cuando una matriz es involutiva, la multiplicación de la matriz por la propia matriz da como resultado la matriz identidad. Fíjate en la demostración:

Cualquier matriz multiplicada por su inversa da la matriz Identidad (o Unidad). Por lo tanto:

$\displaystyle A \cdot A^{-1} = I$

Y como la inversa de una matriz involutiva es la propia matriz:

$\displaystyle A \cdot A = I$

Por tanto, una matriz involutiva elevado al cuadrado da la matriz identidad:

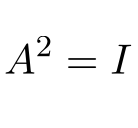
Ejemplos de matrices involutivas

Ejemplo de matriz involutiva 2×2:

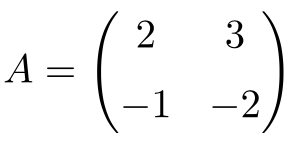
ejemplo de matriz involutiva de dimension 2x2

Podemos comprobar que se trata de una matriz involutiva calculando la segunda potencia de la matriz:

$\displaystyle A^2=\begin{pmatrix} 2 & 3 \\[1.1ex] -1 & -2 \end{pmatrix} \cdot \begin{pmatrix} 2 & 3 \\[1.1ex] -1 & -2 \end{pmatrix}= \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}$

Como la matriz A al cuadrado es la matriz identidad, la matriz A es una matriz involutiva 2×2.

Ejemplo de matriz involutiva 3×3:

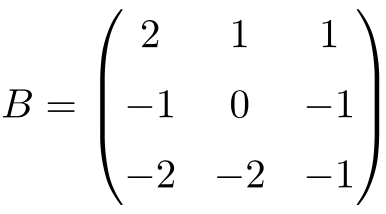
ejemplo de matriz involutiva de dimension 3x3

Podemos comprobar que se trata de una matriz involutiva resolviendo el producto de la matriz por ella misma:

$\displaystyle B^2=\begin{pmatrix} 2 & 1 & 1 \\[1.1ex] -1 & 0 & -1 \\[1.1ex] -2 & -2 & -1 \end{pmatrix}\cdot \begin{pmatrix} 2 & 1 & 1 \\[1.1ex] -1 & 0 & -1 \\[1.1ex] -2 & -2 & -1 \end{pmatrix}= \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

Como la matriz B al cuadrado es la matriz identidad, la matriz B es una matriz involutiva 3×3.

Ejemplo de matriz involutiva 4×4:

La matriz Identidad (o Unidad), sea de la dimensión que sea, es una matriz involutiva por definición.

$\displaystyle I=\begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex]0 & 1 & 0 & 0\\[1.1ex]0 & 0 & 1 & 0 \\[1.1ex]0 & 0 & 0 & 1 \end{pmatrix}$

Podemos comprobar que se trata de una matriz involutiva elevando la matriz a la 2:

$\displaystyle I^2=\begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex]0 & 1 & 0 & 0\\[1.1ex]0 & 0 & 1 & 0 \\[1.1ex]0 & 0 & 0 & 1 \end{pmatrix}\cdot \begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex]0 & 1 & 0 & 0\\[1.1ex]0 & 0 & 1 & 0 \\[1.1ex]0 & 0 & 0 & 1 \end{pmatrix}= \begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex]0 & 1 & 0 & 0\\[1.1ex]0 & 0 & 1 & 0 \\[1.1ex]0 & 0 & 0 & 1 \end{pmatrix}$

Como la matriz Identidad al cuadrado es la matriz identidad, la matriz identidad es una matriz involutiva 4×4.

Evidentemente, la matriz identidad puede ser de cualquier dimensión, ya que es simplemente una matriz diagonal con todo 1 en la diagonal principal y el resto 0. De manera que la matriz identidad siempre será una matriz involutiva, independientemente del orden del que sea.

Fórmula de la matriz involutiva

Una de las propiedades de la matriz involutiva es que se puede saber su fórmula. Pero la demostración de la fórmula de una matriz involutiva de segundo orden es bastante tediosa, así que te vamos a dejar directamente con el resultado, que es lo verdaderamente importante. Si estás más interesad@ en la demostración, puedes verla explicada paso a paso abajo en los comentarios.

La fórmula de una matriz involutiva de dimensión 2×2 es la siguiente:

Por tanto, cualquier matriz cuyos valores de la diagonal principal sean opuestos y su determinante sea -1, será una matriz involutiva.

Sin embargo, además de las matrices descritas por esta fórmula, debes de tener en cuenta que la matriz identidad y su opuesta también son matrices involutivas de orden 2:

$\displaystyle \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix} \qquad \begin{pmatrix} -1 & 0 \\[1.1ex] 0 & -1 \end{pmatrix}$

Propiedades de una matriz involutiva

Las matrices involutivas tienen las siguientes características:

El determinante de una matriz involutiva siempre es igual a -1 o +1.

Existe una relación entre las matrices involutivas y las matrices idempotentes: la matriz $A$ es involutiva si, y solo si, la matriz $\displaystyle Q= \cfrac{1}{2} \cdot (A+I)$ es idempotente.

Si $A$ y $B$ son dos matrices involutivas que conmutan entre sí, entonces el producto matricial $AB$ también es otra matriz involutiva.

Cualquier potencia de una matriz involutiva da como resultado otra matriz involutiva. En particular, una matriz involutiva elevada a un exponente impar será igual a ella misma, en cambio, si está elevada a un exponente par será equivalente a la matriz Identidad.

$A^2 = I$

$A^3 = A$

Matrices y Determinantes

08/11/2021 a las 10:54

Hola Jessica, te dejo la demostración de la fórmula de una matriz involutiva 2×2 a continuación.

Sea A una matriz cualquiera:
$A=\begin{pmatrix}a&b\\[1.1ex]c&d\end{pmatrix}$

Para que una matriz sea involutiva su inversa debe ser igual a dicha matriz, por lo que se debe cumplir la siguiente ecuación matricial:
$A=A^{-1}$

Utilizando la fórmula de la matriz inversa 2×2, la ecuación matricial queda:
$\begin{pmatrix}a&b\\[1.1ex]c&d\end{pmatrix}=\cfrac{1}{ad-cb}\begin{pmatrix}d&-b\\[1.1ex]-c&a\end{pmatrix}$

De modo que se deben cumplir las siguientes cuatro ecuaciones:

$a=\cfrac{d}{ad-cb}$

$b=\cfrac{-b}{ad-cb}$

$c=\cfrac{-c}{ad-cb}$

$d=\cfrac{a}{ad-cb}$

Si te fijas bien, la segunda y la tercera ecuación solo se cumplen si el denominador es -1, cuya expresión corresponde al determinante de la matriz A, por lo tanto, el determinante de la matriz debe ser -1. Y cuando se da esta condición las ecuaciones quedan de la siguiente manera:

$a=-d$

$b=b$

$c=c$

$d=-a$

Y de esta forma llegamos a la fórmula de la matriz involutiva 2×2: el elemento d debe ser el negativo de a, los elementos b y c pueden ser cualesquiera, y el determinante de la matriz tiene que ser igual a -1.

$\displaystyle A=\begin{pmatrix}a&b\\[1.1ex]c&-a\end{pmatrix} \qquad det(A)=-1$

Responder

4 comentarios en “Matriz Involutiva”

Jimena
24/06/2021 a las 21:15

Muchas gracias ☺️

Responder
1. Matrices y Determinantes
  28/06/2021 a las 20:09
  
  ¡Gracias a ti Jimena!
  
  Responder
Jessica Alexandra Santos Contreras
04/11/2021 a las 03:33

Muchas gracias! Disculpa, no he sabido como demostrar la fórmula de esta matriz en el caso 2×2 ¿me podrías ayudar?

Responder
1. Matrices y Determinantes
  08/11/2021 a las 10:54
  
  Hola Jessica, te dejo la demostración de la fórmula de una matriz involutiva 2×2 a continuación.
  
  Sea A una matriz cualquiera:
  $A=\begin{pmatrix}a&b\\[1.1ex]c&d\end{pmatrix}$
  
  Para que una matriz sea involutiva su inversa debe ser igual a dicha matriz, por lo que se debe cumplir la siguiente ecuación matricial:
  $A=A^{-1}$
  
  Utilizando la fórmula de la matriz inversa 2×2, la ecuación matricial queda:
  $\begin{pmatrix}a&b\\[1.1ex]c&d\end{pmatrix}=\cfrac{1}{ad-cb}\begin{pmatrix}d&-b\\[1.1ex]-c&a\end{pmatrix}$
  
  De modo que se deben cumplir las siguientes cuatro ecuaciones:
  
  $a=\cfrac{d}{ad-cb}$
  
  $b=\cfrac{-b}{ad-cb}$
  
  $c=\cfrac{-c}{ad-cb}$
  
  $d=\cfrac{a}{ad-cb}$
  
  Si te fijas bien, la segunda y la tercera ecuación solo se cumplen si el denominador es -1, cuya expresión corresponde al determinante de la matriz A, por lo tanto, el determinante de la matriz debe ser -1. Y cuando se da esta condición las ecuaciones quedan de la siguiente manera:
  
  $a=-d$
  
  $b=b$
  
  $c=c$
  
  $d=-a$
  
  Y de esta forma llegamos a la fórmula de la matriz involutiva 2×2: el elemento d debe ser el negativo de a, los elementos b y c pueden ser cualesquiera, y el determinante de la matriz tiene que ser igual a -1.
  
  $\displaystyle A=\begin{pmatrix}a&b\\[1.1ex]c&-a\end{pmatrix} \qquad det(A)=-1$
  
  Responder