En esta página encontrarás la explicación de una matriz regular o invertible y cómo saber cuándo se puede realizar la inversión de una matriz y cuándo no. Además, también verás varios ejemplos de matrices regulares para entender perfectamente el concepto y, finalmente, te mostramos todas las propiedades de este tipo de matriz.
¿Qué es una matriz regular?
La definición de matriz regular es la siguiente:
Una matriz regular es una matriz cuadrada que se puede invertir, es decir, que se puede calcular la inversa de dicha matriz. Por lo tanto, su determinante es diferente de cero (0).
A las matrices regulares también se les llama matrices invertibles, no singulares o no degeneradas.
La matriz opuesta a la matriz regular es la matriz singular o degenerada.
De manera que para saber cuándo una matriz es regular o singular, es decir, cuándo una matriz es invertible o no, tan solo hace falta resolver el determinante de la matriz:
- Si el determinante de la matriz es distinto de cero, la matriz es regular o invertible.
- Si el determinante de la matriz es igual a cero, la matriz es singular o no invertible.
En conclusión, calcular el determinante de una matriz es la manera más fácil de saber si la matriz tiene inversa o no, así que es lo que recomendamos para determinar la invertibilidad de cualquier matriz.
Si quieres saber cómo se invierte una matriz puedes consultar la fórmula de la matriz inversa, donde se explica paso a paso cómo invertir una matriz, y también encontrarás varios ejemplos y ejercicios resueltos para poder practicar.
Ejemplos de matrices regulares o invertibles
Una vez visto el significado de matriz regular o invertible, veamos algunos ejemplos de matrices regulares de varias dimensiones:
Ejemplo de matriz regular o invertible 2×2
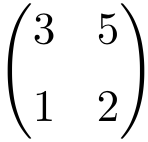
Podemos comprobar que se trata de una matriz regular calculando su determinante:
El determinante de la matriz de orden 2 es distinto de 0, por lo que es una matriz regular.
Ejemplo de matriz regular o invertible 3×3
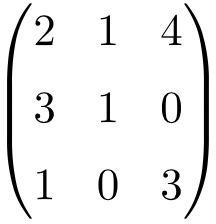
Debemos hacer el determinante de la matriz para verificar que es una matriz invertible:
El determinante de la matriz de orden 3 da como resultado diferente de 0, por lo tanto, se trata de una matriz regular.
Ejemplo de matriz regular o invertible 4×4

Al sacar el determinante de la matriz se demuestra que es una matriz regular:
El determinante de la matriz de orden 4 no es nulo, así que se trata de una matriz invertible.
Atención: Si tienes dudas sobre los cálculos de los determinantes, puedes consultar la página de cómo calcular un determinante.
Propiedades de las matrices regulares o invertibles
Las matrices regulares o invertibles son muy importantes para el Álgebra lineal, y eso es debido a las siguientes características:
- Si A es una matriz invertible, también lo es su matriz traspuesta o transpuesta. Además, la matriz inversa de la traspuesta es igual a la transpuesta de la inversa.
- El rango de una matriz regular siempre es el máximo posible, o dicho de otra forma, el rango es equivalente a la dimensión de la matriz.
- El producto matricial entre dos matrices invertibles da lugar a otra matriz regular. Esta condición se puede demostrar fácilmente con las propiedades de los determinantes:
- Cualquier matriz ortogonal es al mismo tiempo una matriz regular.
- Sea A la matriz que representa un sistema de ecuaciones lineales
, si A es una matriz regular el sistema tiene una única solución, por lo que es un Sistema Compatible Determinante (SCD).
- Además, si el sistema es un sistema homogéneo
y A se puede invertir, la solución del sistema es trivial:
- Las columnas y las filas de una matriz regular son linealmente independientes entre sí.
- Todos los valores propios (o autovalores) de una matriz regular o invertible son distintos de cero.


gracias
¡Un placer Pedro! 😉
Hola buenas noches quiero saber cuando una matriz no es invertible de A=a b
a b
Hola Silvina, no acabo de entender la ecuación matricial que propones.
Pero para averiguar si una matriz se puede invertir basta con calcular el determinante de la matriz: