Matriz Jacobiana y Jacobiano

En esta página encontrarás qué es la matriz Jacobiana y cómo calcularla mediante un ejemplo. Además, tienes varios ejercicios resueltos de matrices Jacobianas para que puedas practicar. También verás por qué es tan importante el determinante de la matriz Jacobiana, el Jacobiano. Finalmente, explicamos las relaciones que tiene esta matriz con otras operaciones y las aplicaciones que tiene.

Sumario
1. ¿Qué es la matriz Jacobiana?
2. Ejemplo de cómo calcular la matriz Jacobiana
3. Ejercicios resueltos de matrices Jacobianas
4. Determinante de la matriz Jacobiana: el Jacobiano
5. El Jacobiano y la invertibilidad de una función
6. Relación de la matriz Jacobiana con otras operaciones
7. Aplicaciones de la matriz Jacobiana

¿Qué es la matriz Jacobiana?

La definición de la matriz Jacobiana es la siguiente:

La matriz Jacobiana es una matriz formada por las derivadas parciales de primer orden de una función.

De manera que la fórmula de la matriz Jacobiana es la siguiente:

formula de la matriz jacobiana

Por tanto, las matrices Jacobianas siempre tendrán tantas filas como funciones escalares (f_1,f_2,\ldots ,f_m) tenga la función, y el número de columnas coincidirá con el número de variables (x_1, x_2, \ldots , x_n).

Por otro lado, a esta matriz también se la conoce como diferencial jacobiana o aplicación lineal jacobiana. De hecho, a veces también se escribe con la letra D en vez de la letra J:

\displaystyle J_f = D_f

Como curiosidad, la matriz Jacobiana recibe este nombre en honor a Carl Gustav Jacobi, un importante matemático y profesor del siglo XIX que hizo importantes contribuciones al mundo de las matemáticas, especialmente en el campo del álgebra lineal.

Ejemplo de cómo calcular la matriz Jacobiana

Una vez visto el concepto de la matriz Jacobiana, vamos a ver paso a paso cómo se calcula mediante un ejemplo:

  • Determina la matriz Jacobiana en el punto (1,2) de la siguiente función:

\displaystyle f(x,y)= (x^4 +3y^2x \ , \ 5y^2-2xy+1)

Lo primero que debemos hacer es calcular todas las derivadas parciales de primer orden de la función:

\displaystyle \cfrac{\partial f_1}{\partial x} = 4x^3+3y^2

\displaystyle \cfrac{\partial f_1}{\partial y} = 6yx

\displaystyle \cfrac{\partial f_2}{\partial x} = -2y

\displaystyle \cfrac{\partial f_2}{\partial y} = 10y-2x

Ahora aplicamos la fórmula de la matriz Jacobiana. En este caso la función tiene dos variables y dos funciones escalares, por lo que la matriz Jacobiana será una matriz cuadrada de dimensión 2×2:

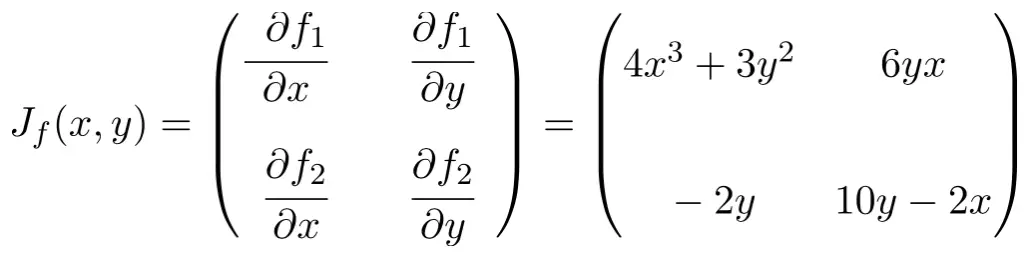
Una vez tenemos la expresión de la matriz Jacobiana, la evaluamos en el punto (1,2):

\displaystyle J_f(1,2)=\begin{pmatrix} 4\cdot 1^3+3\cdot 2^2 & 6\cdot 2 \cdot 1 \\[3ex] -2\cdot 2 & 10\cdot 2-2 \cdot 1 \end{pmatrix}

Y, finalmente, realizamos las operaciones y obtenemos la solución:

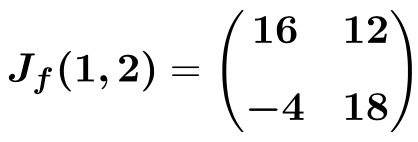
ejemplo de calcular la matriz jacobiana

Una vez visto cómo hallar la matriz Jacobiana de una función, te dejamos con varios ejercicios resueltos paso a paso para que puedas practicar.

Ejercicios resueltos de matrices Jacobianas

Ejercicio 1

Halla la matriz Jacobiana en el punto (0,-2) de la siguiente función vectorial con 2 variables:

\displaystyle f(x,y)= (e^{xy}+y \ , \ y^2x)

La función tiene dos variables y dos funciones escalares, por lo que la matriz Jacobiana será una matriz cuadrada de tamaño 2×2:

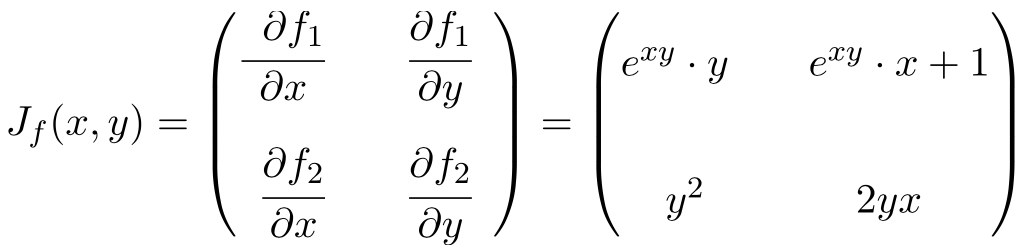
ejercicio resuelto de matriz Jacobiana

Una vez hemos calculado la expresión de la matriz Jacobiana, la evaluamos en el punto (0,-2):

\displaystyle J_f(0,-2)=\begin{pmatrix}e^{0\cdot (-2)}\cdot (-2)\phantom{5} & \phantom{5}e^{0\cdot (-2)} \cdot 0 +1 \\[4ex](-2)^2 & 2\cdot (-2) \cdot 0 \end{pmatrix}

Y, finalmente, realizamos las operaciones y obtenemos el resultado:

\displaystyle \bm{J_f(0,-2)}=\begin{pmatrix} \bm{-2} & \bm{1} \\[1.5ex] \bm{4} & \bm{0} \end{pmatrix}

 

Ejercicio 2

Calcula la matriz Jacobiana en el punto (2,-1) de la siguiente función con 2 variables:

\displaystyle f(x,y)= (x^3y^2 - 5x^2y^2 \ , \ y^6-3y^3x+7)

En este caso la función tiene dos variables y dos funciones escalares, por lo tanto, la matriz Jacobiana será una matriz cuadrada de orden 2:

\displaystyle J_f(x,y)=\begin{pmatrix}\cfrac{\phantom{5}\partial f_1}{\partial x}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial y}\phantom{5} \\[3ex] \cfrac{\partial f_2}{\partial x} & \cfrac{\partial f_2}{\partial y}\end{pmatrix} = \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}}3x^2y^2-10xy^2& 2x^3y-10x^2y \\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}} -3y^3 & 6y^5-9y^2x \end{pmatrix}

Una vez hemos hallado la expresión de la matriz Jacobiana, la evaluamos en el punto (2,-1):

\displaystyle J_f(2,-1)=\begin{pmatrix} 3\cdot 2^2\cdot (-1)^2-10\cdot 2 \cdot (-1)^2\phantom{5} & \phantom{5}2\cdot 2^3\cdot (-1)-10\cdot 2^2\cdot (-1) \\[4ex] -3(-1)^3 & 6\cdot (-1)^5-9\cdot (-1)^2\cdot 2 \end{pmatrix}

Y, por último, realizamos las operaciones y obtenemos el resultado:

\displaystyle \bm{J_f(1,2)}=\begin{pmatrix} \bm{-8} & \bm{24} \\[1.5ex] \bm{3} & \bm{-24} \end{pmatrix}

 

Ejercicio 3

Determina la matriz Jacobiana en el punto (2,-2,2) de la siguiente función con 3 variables:

\displaystyle f(x,y,z)= \left(z\tan (x^2-y^2) \ , \ xy\ln \left( \frac{z}{2} \right)\right)

En este caso la función tiene tres variables y dos funciones escalares, por lo tanto, la matriz Jacobiana será una matriz rectangular de dimensión 2×3:

\displaystyle J_f(x,y,z)= \begin{pmatrix}\cfrac{\phantom{5}\partial f_1}{\partial x}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial y}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial z}\phantom{5} \\[3ex] \cfrac{\partial f_2}{\partial x} & \cfrac{\partial f_2}{\partial y} &\cfrac{\partial f_2}{\partial z}\end{pmatrix}

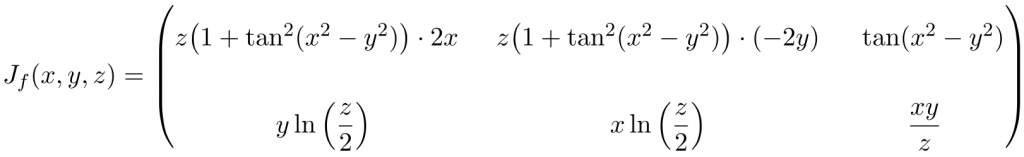
matriz jacobiana ejercicio resuelto de 3 variables

Una vez ya tenemos la expresión de la matriz Jacobiana, la evaluamos en el punto (2,-2,2):

\displaystyle J_f(2,-2,2)= \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}}2\bigl(1+\tan^2 (2^2-(-2)^2)\bigr) \cdot 2\cdot 2 & 2\bigl(1+\tan^2 (2^2-(-2)^2)\bigr) \cdot (-2\cdot (-2)) & \tan (2^2-(-2)^2)\\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}} \displaystyle -2\ln \left( \frac{2}{2} \right) & \displaystyle 2\ln \left( \frac{2}{2} \right) &\displaystyle \frac{2\cdot (-2)}{2} \right)\end{pmatrix}

Realizamos los cálculos:

\displaystyle J_f(2,-2,2)= \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}}2\bigl(1+\tan^2 (0)\bigr) \cdot 4 \phantom{5} & 2\bigl(1+\tan^2 (0)\bigr) \cdot 4 & \phantom{5}\tan (0)\\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}} -2\cdot 0 & 2\cdot 0 &-2 \right)\end{pmatrix}

Y seguimos operando hasta que no se pueda simplificar más:

\displaystyle \bm{J_f(2,-2,2)=} \begin{pmatrix}\bm{8} & \bm{8} & \bm{0} \\[2ex] \bm{0} & \bm{0} &\bm{-2} \right)\end{pmatrix}

 

Ejercicio 4

Determina la matriz Jacobiana en el punto (\pi, \pi) de la siguiente función multivariable:

\displaystyle f(x,y)= \left( \frac{\cos (x-y)}{x} \ , \ e^{x^2-y^2} \ , \ x^3\sin (2y) \right)

En este caso la función tiene dos variables y tres funciones escalares, por lo tanto, la matriz Jacobiana será una matriz rectangular de dimensión 3×2:

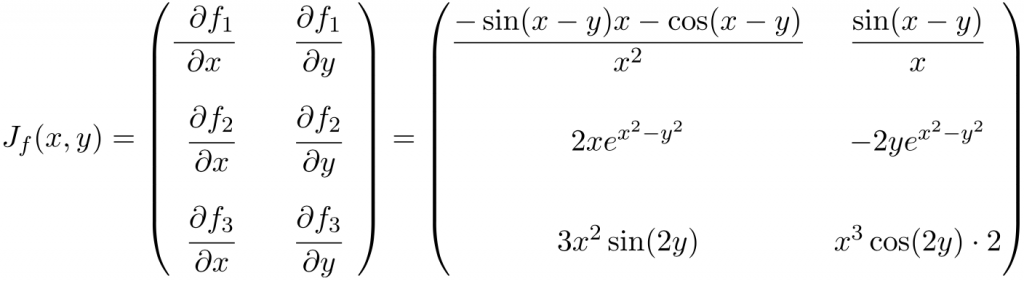
ejercicio resuelto paso a paso de matriz jacobiana

Una vez ya tenemos la expresión de la matriz Jacobiana, la evaluamos en el punto (\pi, \pi):

\displaystyle J_f(\pi,\pi)= \begin{pmatrix} \displaystyle \vphantom{\cfrac{\partial f_3}{\partial y}}\frac{-\sin(\pi-\pi)\pi-\cos(\pi-\pi)}{\pi^2} & \displaystyle\frac{\sin (\pi- \pi)}{\pi} \\[3ex] \vphantom{\cfrac{\partial f_3}{\partial y}}2\pi e^{\pi^2-\pi^2} & -2\pi e^{\pi^2-\pi^2} \\[3ex] \vphantom{\cfrac{\partial f_3}{\partial y}} 3\pi^2\sin(2\pi) & \pi^3 \cos(2\pi)\cdot 2 \end{pmatrix}

Realizamos las operaciones:

\displaystyle J_f(\pi,\pi)= \begin{pmatrix} \displaystyle \vphantom{\cfrac{\partial f_3}{\partial y}}\displaystyle\frac{-0-1}{\pi^2} & \displaystyle\frac{0}{\pi} \\[3ex] \vphantom{\cfrac{\partial f_3}{\partial y}}2\pi e^{0} & -2\pi e^{0} \\[3ex] \vphantom{\cfrac{\partial f_3}{\partial y}} 3\pi^2\cdot 0 & \pi^3 \cdot 1 \cdot 2 \end{pmatrix}

De manera que la matriz Jacobiana de la función vectorial en el punto en cuestión vale:

\displaystyle \bm{J_f(\pi,\pi)=} \begin{pmatrix}\displaystyle -\frac{\bm{1}}{\bm{\pi^2}} & \bm{0} \\[3ex] \bm{2\pi} & \bm{-2\pi}\\[3ex]\bm{0} & \bm{2\pi^3} \right)\end{pmatrix}

 

Ejercicio 5

Calcula la matriz Jacobiana en el punto (3,0,\pi) de la siguiente función con 3 variables:

\displaystyle f(x,y,z)= \left(xe^{2y}\cos(-z) \ , \ (y-2)^3\cdot \sin\left(\frac{z}{2}\right) \ , \ e^{2y}\cdot \ln\left(\frac{x}{3}\right) \right)

En este caso la función es de tres variables y tres funciones escalares, por lo tanto, la matriz Jacobiana será una matriz cuadrada de dimensión 3×3:

\displaystyle J_f(x,y,z)=\begin{pmatrix}\phantom{5}\cfrac{\partial f_1}{\partial x}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial y}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial z}\phantom{5} \\[3ex] \cfrac{\partial f_2}{\partial x} & \cfrac{\partial f_2}{\partial y} & \cfrac{\partial f_2}{\partial z} \\[3ex] \cfrac{\partial f_3}{\partial x} & \cfrac{\partial f_3}{\partial y} & \cfrac{\partial f_3}{\partial z}\end{pmatrix}

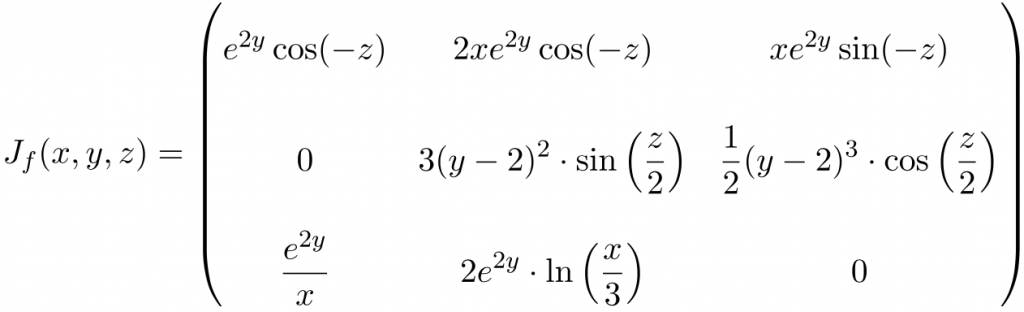
ejercicio resuelto de matriz jacobiana 3x3 con 3 variables

Una vez hemos hallado la matriz Jacobiana, la evaluamos en el punto (3,0,\pi):

\displaystyle J_f(3,0,\pi)= \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}} e^{2\cdot 0}\cos(-\pi) & 2\cdot 3e^{2\cdot 0}\cos(-\pi) & 3e^{2\cdot 0}\sin(-\pi) \\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}} 0 & \displaystyle 3(0-2)^2\cdot \sin\left(\frac{\pi}{2}\right) & \displaystyle\frac{1}{2}(0-2)^3\cdot \cos\left(\frac{\pi}{2}\right)\\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}}\displaystyle\frac{e^{2\cdot 0}}{3} &\displaystyle 2e^{2\cdot 0}\cdot \ln\left(\frac{3}{3}\right) & 0\end{pmatrix}

Calculamos las operaciones:

\displaystyle J_f(3,0,\pi)= \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}} 1\cdot (-1) & 6\cdot 1\cdot (-1) & 3\cdot 1 \cdot 0 \\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}} 0 & \displaystyle 3\cdot 4 \cdot 1 & \displaystyle\frac{1}{2}\cdot (-8)\cdot 0\\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}}\displaystyle\frac{1}{3} &\displaystyle 2\cdot 1\cdot 0 & 0\end{pmatrix}

Y el resultado de la matriz Jacobiana en el punto es:

\displaystyle \bm{J_f(3,0,\pi)=} \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}} \bm{-1} & \bm{-6} & \phantom{-}\bm{0} \\[2ex] \bm{0} & \bm{12} & \displaystyle \bm{0} \\[2ex] \displaystyle \frac{\bm{1}}{\bm{3}} &\bm{0}& \bm{0}\end{pmatrix}

 

Determinante de la matriz Jacobiana: el Jacobiano

Al determinante de la matriz Jacobiana se le llama Jacobiano o determinante Jacobiano. Hay que tener en cuenta que el Jacobiano solo se podrá calcular si la función tiene el mismo número de variables que de funciones escalares, ya que entonces la matriz Jacobiana tendrá el mismo número de filas que de columnas y, en consecuencia, será una matriz cuadrada.

Ejemplo de Jacobiano

Veamos un ejemplo de cómo calcular el determinante Jacobiano de una función con dos variables:

\displaystyle f(x,y)= (x^2-y^2 \ , \ 2xy)

En primer lugar calculamos la matriz Jacobiana de la función:

\displaystyle J_f(x,y)=\begin{pmatrix}\cfrac{\phantom{5}\partial f_1}{\partial x}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial y}\phantom{5} \\[3ex] \cfrac{\partial f_2}{\partial x} & \cfrac{\partial f_2}{\partial y}\end{pmatrix} = \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}}2x \phantom{5}& -2y \\[2ex] \vphantom{\cfrac{\partial f_2}{\partial x}} 2y & 2x \end{pmatrix}

Y ahora resolvemos el determinante de la matriz 2×2:

\displaystyle \text{det}\bigl(J_f(x,y)\bigr) =\begin{vmatrix} 2x&-2y \\[2ex] 2y & 2x \end{vmatrix} = \bm{4x^2+4y^2}

El Jacobiano y la invertibilidad de una función

Ahora que has visto el concepto del Jacobiano, seguro que has pensado… ¿y para qué sirve?

Pues bien, la principal utilidad del Jacobiano es determinar si se puede invertir una función. El teorema de la función inversa dice que si el determinante de la matriz Jacobiana (el Jacobiano) es diferente de 0, significa que esa función es invertible.

\displaystyle \text{det}\bigl(J_f\bigr) \neq 0 \ \longrightarrow \ \exists \ f^{-1}

Hay que remarcar que esta condición es necesaria pero no suficiente, es decir, si el determinante es distinto de cero podemos afirmar que se puede invertir la matriz, sin embargo, si el determinante es igual a 0 no podemos saber si la función tiene inversa o no.

Por ejemplo, en el ejemplo visto antes de cómo hallar el Jacobiano de una función, el determinante da 4x^2+4y^2. En ese caso podemos afirmar que la función se puede invertir siempre excepto en el punto (0,0), porque este punto es el único en el que el determinante Jacobiano es igual a cero y, por lo tanto, desconocemos si existe la función inversa en este punto.

Relación de la matriz Jacobiana con otras operaciones

La matriz Jacobiana tiene relación con el gradiente y la matriz Hessiana de una función:

Gradiente

Si la función se trata de una función escalar, la matriz Jacobiana será una matriz fila que será equivalente al gradiente:

\displaystyle f: \mathbb{R}^n \to \mathbb{R}

\displaystyle J_f = \nabla f = \begin{pmatrix}\phantom{5} \cfrac{\partial f}{\partial x_1} \phantom{5}& \cfrac{\partial f}{\partial x_2}& \dots & \cfrac{\partial f}{\partial x_n}\phantom{5} \end{pmatrix}

Matriz Hessiana

La matriz Jacobiana del gradiente de una función es igual a la matriz Hessiana:

\displaystyle H_f = J(\nabla f)

El Hessiano es una matriz muy importante para la derivación de funciones con más de una variable, ya que está formada por las segundas derivadas de la función. De hecho, podríamos decir que la matriz Hessiana es la continuidad de la matriz Jacobiana. Pero es tan importante que tenemos toda una página explicándola al detalle. De modo que si estás interesad@ en saber bien qué es esta matriz y por qué es tan especial puedes hacer click en el link.

Aplicaciones de la matriz Jacobiana

Además de la utilidad que hemos visto del Jacobiano, el cual nos determina si una función es invertible, la matriz Jacobiana tiene otras aplicaciones.

La matriz Jacobiana sirve para calcular los puntos críticos de una función multivarible, que luego se clasifican en máximos, mínimos o puntos de silla a través de la matriz Hessiana. Para hallar los puntos críticos se tiene que calcular la matriz Jacobiana de la función, igualarla a 0 y resolver las ecuaciones resultantes.

\displaystyle J_f(x)=0

Además, otra aplicación de la matriz Jacobiana se encuentra en la integración de funciones con más de una variable, es decir en integrales dobles, triples, etc. Ya que el determinante de la matriz Jacobiana permite hacer un cambio de variable en las integrales múltiples según la siguiente fórmula:

\displaystyle x=T(x^*)

\displaystyle \int_\Omega f(x)dx=\int_{\Omega^*} f\bigl(T(x^*)\bigr)\cdot \begin{vmatrix} \text{det}\bigl(JT(x^*)\bigr)\end{vmatrix} dx^*

Donde T es la función de cambio de variable que relaciona las variables originales con las nuevas.

Finalmente, la matriz Jacobiana también sirve para hacer una aproximación lineal de cualquier función f entorno a un punto p:

\displaystyle f(x) \approx f(p) + J_f(p)(x-p)

Deja un comentario

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *

Ir arriba