En esta página explicamos qué son las matrices idempotentes. También te mostramos varios ejemplos de este tipo de matrices para que lo entiendas perfectamente. Además, encontrarás la fórmula para hallar una matriz idempotente y, finalmente, todas las propiedades de las matrices idempotentes.
¿Qué es una matriz idempotente?
La definición de matriz idempotente es la siguiente:
Una matriz idempotente es aquella matriz que multiplicada por ella misma da como resultado la misma matriz.
Por lo tanto, cualquier potencia de una matriz idempotente es igual a la propia matriz, independientemente del exponente:
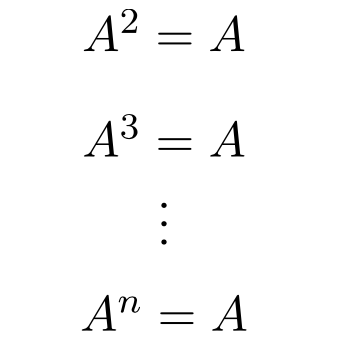
De hecho, por esta razón este tipo de matriz recibe este nombre. Porque en matemáticas la idempotencia es una operación que significa que siempre se obtiene el mismo resultado independientemente del número de veces que se realice.
Ejemplos de matrices idempotentes
Una vez ya conocemos el concepto de matriz idempotente, vamos a ver algunos ejemplos de diferentes dimensiones para acabarlo de entender.
Ejemplo de matriz idempotente 2×2
La siguiente matriz cuadrada de dimensión 2×2 es idempotente:
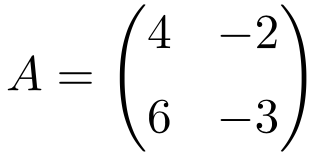
Para comprobar que es una matriz idempotente calculamos su cuadrado:
![\displaystyle A^2=\begin{pmatrix} 4 &-2 \\[1.1ex] 6 & -3 \end{pmatrix}](https://www.matricesydeterminantes.com/wp-content/ql-cache/quicklatex.com-5be1fbffed9fdc5a58f95f2fd1b694c1_l3.svg "Rendered by QuickLaTeX.com")
El resultado es idéntico, por lo que queda demostrado que se trata de una matriz idempotente.
Ejemplo de matriz idempotente 3×3
La siguiente matriz cuadrada de tamaño 3×3 es idempotente:
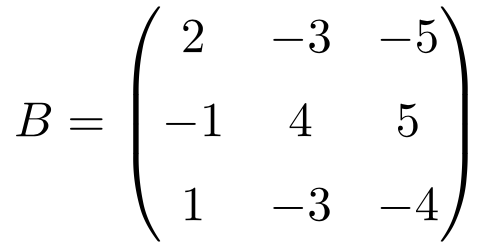
Para verificar que realmente corresponde una matriz idempotente elevamos la matriz a la 2:
![\displaystyle B^2=\begin{pmatrix} 2 &-3 & -5 \\[1.1ex] -1 & 4 & 5 \\[1.1ex] 1 & -3 & -4 \end{pmatrix}](https://www.matricesydeterminantes.com/wp-content/ql-cache/quicklatex.com-6f969e849672565c5711a5c917eb2afc_l3.svg "Rendered by QuickLaTeX.com")
El resultado es el mismo que la matriz original, así que se demuestra la idempotencia de la matriz.
Estructura de una matriz idempotente 2×2
A continuación te mostramos la fórmula para obtener una matriz idempotente. Por si estás más interesad@, puedes ver la demostración de la fórmula más abajo en los comentarios, pero es un poco tediosa así que aquí te dejamos directamente con la fórmula de las matrices idempotentes:
De manera que los elementos de la diagonal secundaria de una matriz idempotente pueden ser cualesquiera mientras se cumpla la condición 
y los números de la diagonal principal deben ser 
y 
Además de todas las matrices descritas por esta fórmula, hay que añadir la matriz Identidad, que también es una matriz idempotente pese a no cumplir con la fórmula. Si no sabes qué matriz es, puedes consultar cuál es la matriz Identidad.
Propiedades de las matrices idempotentes
Las matrices idempotentes tienen las siguientes características:
- El determinante de una matriz idempotente siempre da como resultado 0 o 1.
- Excepto la matriz Identidad, todas las otras matrices idempotentes son a la vez matrices singulares o degeneradas, es decir, no son invertibles.
- Cualquier matriz idempotente es diagonalizable, y sus autovalores (o valores propios) siempre son 0 o 1.
- La traza de una matriz idempotente es igual al rango de la matriz.
- Por último, existe una relación entre las matrices idempotentes y las matrices involutivas: la matriz
es idempotente si, y solo si, la matriz 
es involutiva.
Donde puedo encontrar la demostración de la formula para obtener matrices idempotentes?
Hola Pedro, te voy a demostrar la fórmula de las matrices idempotentes a continuación.
Para que una matriz sea idempotente se debe cumplir la siguiente ecuación:
Sea A una matriz 2×2 cualquiera:
![\displaystyle A=\begin{pmatrix}a&b\\[1.1ex]c&d\end{pmatrix}](https://www.matricesydeterminantes.com/wp-content/ql-cache/quicklatex.com-628bab003b152caa462b7e956c23942a_l3.svg "Rendered by QuickLaTeX.com")
Entonces, la ecuación matricial queda:
![\begin{pmatrix}a&b\\[1.1ex]c&d\end{pmatrix}\cdot \begin{pmatrix}a&b\\[1.1ex]c&d\end{pmatrix}=\begin{pmatrix}a&b\\[1.1ex]c&d\end{pmatrix}](https://www.matricesydeterminantes.com/wp-content/ql-cache/quicklatex.com-f459e3132cd60dbce73aca74f9dc556a_l3.svg "Rendered by QuickLaTeX.com")
Resolvemos el producto matricial:
![\begin{pmatrix}a^2+bc&ab+bd\\[1.1ex] ca+dc&bc+d^2\end{pmatrix}=\begin{pmatrix}a&b\\[1.1ex]c&d\end{pmatrix}](https://www.matricesydeterminantes.com/wp-content/ql-cache/quicklatex.com-3ee545884addd9403556a676bb994092_l3.svg "Rendered by QuickLaTeX.com")
De modo que obtenemos las siguientes igualdades:
![\left.\begin{array}{l}a^2+bc=a\\[2ex]ab+bd=b\\[2ex]ca+dc=c\\[2ex]bc+d^2=d\end{array}\right\}](https://www.matricesydeterminantes.com/wp-content/ql-cache/quicklatex.com-733b3dc2013d4dcbdcac0790e2960a23_l3.svg "Rendered by QuickLaTeX.com")
Ahora podemos deducir la relación entre a y d de la segunda o la tercera ecuación :
Por otro lado, si sustituimos la expresión algebraica obtenida en la cuarta ecuación obtenemos la primera igualdad:
![\begin{array}{l}bc+d^2=d \\[2ex] bc+(1-a)^2=1-a \\[2ex] bc+1+a^2-2a=1-a \\[2ex] a^2+bc=a \end{array}](https://www.matricesydeterminantes.com/wp-content/ql-cache/quicklatex.com-381f56c4f8d3b118779ccd53e740e2cf_l3.svg "Rendered by QuickLaTeX.com")
En conclusión, para que la matriz sea idempotente se deben cumplir las siguientes dos relaciones:
Por lo que todas las matrices idempotentes verifican la siguiente fórmula:
![\begin{pmatrix}a&b\\[1.1ex]c&1-a\end{pmatrix} \quad \text{con} \quad a^2+bc=a](https://www.matricesydeterminantes.com/wp-content/ql-cache/quicklatex.com-ac2f813ca9ce185a887f70329d06f04e_l3.svg "Rendered by QuickLaTeX.com")
Hola, disculpa ¿me puedes colaborar con la demostración de los valores 1 y 0?
Hola Sergio, ¿a qué demostración te refieres? La fórmula de las matrices idempotentes depende de tres variables.
Porque se cumple lo de ser diagonalizable?
Porque todos sus autovectores (o vectores propios) son linealmente independientes. Puedes buscar la explicación detallada de la diagonalización de matrices en nuestra página web.
Hola, podría adjuntar la demostración de donde sale cada propiedad de las matrices idempotentes?
Hola, demostrar todas las propiedades conlleva un gran trabajo y además alargaría demasiado el artículo. Pero puedes comprobar que todas las propiedades expuestas son verdaderas probando si se cumplen las condiciones en ejemplos de matrices idempotentes.
Una pregunta, en la relacion de idempotentes con involutivas, puede resultar que Q sea involutiva, y P sea idempotente si (Q=I -2P), es de un ejercicio que tengo.
Hola Sebastian,
La respuesta es que sí.
Si te fijas en la última propiedad de las matrices idempotentes, dice que la matriz A es idempotente si la matriz P=2A-I es involutiva. Tú estás proponiendo la misma matriz pero cambiada de signo (I-2A), de modo que la única diferencia entre tu matriz y la matriz 2A-I será el signo de sus elementos.
En consecuencia, la matriz I-2A también será involutiva ya que su inversa será la propia matriz.
Hola, una pregunta es valido hacer -P=-I+2A???, en la ultima propiedad de matrices idempotentes
Hola Seabastian de nuevo,
ya te he contestado en el comentario anterior. 🙂
Muchas gracias por el artículo, está excelente! 😀
¿Podrías tal vez agregar un ejemplo de matriz idempotente con determinante = 1?
Muchas gracias! 😀
¡Muchas gracias por tu apoyo Omar!
La matriz identidad (de cualquier dimensión) es un ejemplo de matriz idempotente cuyo determinante es igual a 1.
Más arriba tienes un enlace al artículo en el que se explican las características de este tipo de matriz.
Hola! Hay alguna regla que diga que el producto de dos matrices idempotentes es conmutativo y es igual a la matriz nula, y que la suma de dos matrices idempotentes es igual a la matriz identidad? Estoy haciendo unos ejercicios de la uni y en uno me dieron dos matrices y me pidieron verificar que 1) ambas son idempotentes, 2) el producto de ambas es conmutativo y es igual a la matriz nula, y 3) la suma de ambas es igual a la matriz identidad. Todo se verifica perfectamente. El ejercicio no pide nada más, pero a mi me quedó la duda de si en realidad lo que me estaban pidiendo es verificar unas reglas y esto se cumple siempre. En el apunte que me dieron para estudiar este tema no aparece esto y tal vez me dieron la pista en forma de ejercicio. Me gustaría saber si esto se cumple siempre para dejarmelo anotado o si era un caso especial de este ejercicio.
Gracias de antemano!
Hola Lucía,
En primer lugar, felicitarte por el esfuerzo y la dedicación que pones en tus estudios, ¡si sigues así seguro que consigues muy buena nota!
En cuanto a tu duda, la respuesta a las dos afirmaciones es no. La multiplicación de dos matrices idempotentes no tiene por qué ser conmutativa, y puede dar como resultado una matriz diferente a la matriz nula. Tampoco es cierto el segundo enunciado, la suma de dos matrices de este tipo no siempre da la matriz identidad.
¡Espero que te sea de ayuda!
Hola muchas gracias por la información, una pregunta, ¿el producto de dos matrices idempotentes es idempotente? Gracias
Hola Mari,
La respuesta a tu pregunta es que no, el producto de dos matrices idempotentes no tiene por qué dar otra matriz idempotente.
Por ejemplo, las siguientes dos matrices son idempotentes:
![\begin{pmatrix}4&-2\\[1.1ex] 6&-3\end{pmatrix} \qquad \begin{pmatrix}2&2\\[1.1ex] -1&-1\end{pmatrix}](https://www.matricesydeterminantes.com/wp-content/ql-cache/quicklatex.com-bf4515723ebaa3f8c8a4bbfeb792d03a_l3.svg "Rendered by QuickLaTeX.com")
Así pues, si multiplicamos las dos matrices obtenemos la siguiente matriz 2×2:
![\begin{pmatrix}2&1\\[1.1ex] -1&1\end{pmatrix}\begin{pmatrix}4&-2\\[1.1ex] 6&-3\end{pmatrix}=\begin{pmatrix}14&-7\\[1.1ex] 2&-1\end{pmatrix}](https://www.matricesydeterminantes.com/wp-content/ql-cache/quicklatex.com-2504fcf016ce036e6370a4c48166325f_l3.svg "Rendered by QuickLaTeX.com")
Y, como puedes comprobar a continuación, la matriz resultante del producto no es idempotente:
![\begin{pmatrix}14&-7\\[1.1ex] 2&-1\end{pmatrix}\begin{pmatrix}14&-7\\[1.1ex] 2&-1\end{pmatrix}=\begin{pmatrix}182&-91\\[1.1ex] 26&-13\end{pmatrix}](https://www.matricesydeterminantes.com/wp-content/ql-cache/quicklatex.com-0d5a25d637b740e3928c314142b50002_l3.svg "Rendered by QuickLaTeX.com")