▷ ¿Qué es una matriz Simétrica? (ejemplos y propiedades)

En esta página encontrarás la explicación de qué son las matrices simétricas. Además, te mostramos cómo identificar rápidamente cuándo una matriz es simétrica, así como varios ejemplos para que no te quede ninguna duda. También encontrarás todas las propiedades de las matrices simétricas. Y, finalmente, explicamos una peculiaridad especial que tiene cualquier matriz cuadrada: se puede descomponer en la suma de una matriz simétrica más otra antisimétrica.

Sumario

1. ¿Qué es una matriz simétrica?

2. ¿Cuándo una matriz es simétrica?

3. Ejemplos de matrices simétricas

4. ¿Por qué se llama matriz simétrica?

5. Propiedades de las matrices simétricas

6. Descomposición de una matriz cuadrada en una matriz simétrica y otra antisimétrica

¿Qué es una matriz simétrica?

La definición de matriz simétrica es la siguiente:

Una matriz simétrica es una matriz cuadrada cuya traspuesta es igual a la propia matriz.

$A^t = A$

Donde $A^t$ representa la matriz transpuesta de $A$ .

Una vez ya conocemos el concepto de matriz simétrica, vamos a ver cómo se puede identificar cualquier matriz simétrica de manera fácil:

¿Cuándo una matriz es simétrica?

Reconocer la estructura de una matriz simétrica es muy sencillo: el elemento de la fila i y la columna j tiene que ser idéntico al elemento de la fila j y columna i. Y los valores de la diagonal principal de la matriz pueden ser cualesquiera.

Ejemplos de matrices simétricas

A continuación tienes varios ejemplos de matrices simétricas para acabarlo de entender:

Ejemplo de matriz simétrica de orden 2×2

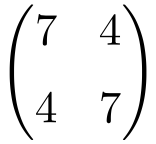
ejemplo de matriz simetrica de dimension 2x2

Ejemplo de matriz simétrica de dimensión 3×3

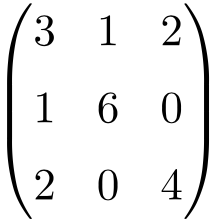
ejemplo de matriz simetrica de dimension 3x3

Ejemplo de matriz simétrica de tamaño 4×4

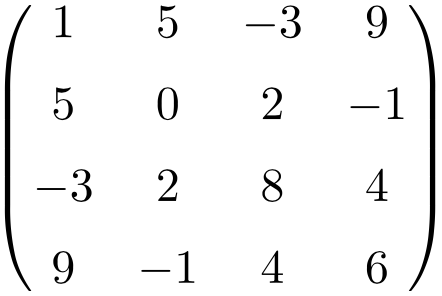
ejemplo de matriz simetrica de dimension 4x4

Al trasponer estas tres matrices se comprueba que son simétricas, porque las matrices traspuestas son equivalentes a sus respectivas matrices originales.

¿Por qué se llama matriz simétrica?

Si te fijas bien en los ejemplos anteriores, la diagonal principal de una matriz simétrica es un eje de simetría, o dicho de otra forma, actúa como un espejo entre los números por encima de la diagonal y los de debajo. Por esta razón este tipo de matrices reciben el nombre de simétricas.

Propiedades de las matrices simétricas

Las características de las matrices simétricas son las siguientes:

La suma (o resta) de dos matrices simétricas da como resultado otra matriz simétrica. Ya que la transposición dos matrices sumadas (o restadas) es equivalente a transponer cada matriz por separado:

$\displaystyle \left(A+B\right)^t = A^t+B^t = A+B$

Cualquier matriz simétrica multiplicada por un escalar también da lugar a otra matriz simétrica.

Del mismo modo, el producto matricial entre dos matrices simétricas no siempre es igual a otra matriz simétrica, tan solo si, y solo si, las dos matrices se pueden conmutar. Esta condición se puede demostrar con la propiedad de la multiplicación de la matriz traspuesta:

$\displaystyle \left(A\cdot B\right)^t = B^t\cdot A^t = BA=AB$

La potencia de una matriz simétrica da lugar a otra matriz simétrica, siempre y cuando el exponente sea un número entero.

Evidentemente, la matriz Unidad y la matriz Nula son ejemplos de matrices simétricas.

Una matriz que es congruente con una matriz simétrica debe ser también simétrica.

Si una matriz simétrica es regular o invertible, entonces su matriz inversa también es simétrica.

Lo mismo sucede con la adjunta de una matriz simétrica: la matriz adjunta de una matriz simétrica da como solución otra matriz simétrica.

Una matriz simétrica real es a la vez una matriz normal.

Como las matrices simétricas son un caso particular de las matrices hermitianas, todos los autovalores (o valores propios) de una matriz simétrica son números reales.

El teorema espectral nos dice que todas las matrices cuyos elementos sean reales son matrices diagonalizables y, además, la diagonalización se realiza mediante una matriz ortogonal. Por lo tanto, todas las matrices simétricas reales se diagonalizan ortogonalmente.

Por otro lado, las matrices simétricas con números complejos se pueden diagonalizar a través de una matriz unitaria.

La matriz Hessiana siempre es simétrica.

Descomposición de una matriz cuadrada en una matriz simétrica y otra antisimétrica

Una peculiaridad de las matrices cuadradas es que se pueden descomponer en la suma de una matriz simétrica más una matriz antisimétrica.

La fórmula que nos permite hacer esto es la siguiente:

$\displaystyle \begin{array}{c} C = S + A \\[2ex] S = \cfrac{1}{2}\cdot (C+C^t) \qquad A = \cfrac{1}{2} \cdot (C-C^t)\end{array}$

Donde C es la matriz cuadrada que queremos descomponer, C^t su traspuesta, y finalmente S y A son las matrices simétrica y antisimiétrica respectivamente en las que se descompone la matriz C.

A continuación tienes ejercicio resuelto para ver cómo se hace. Vamos a descomponer la siguiente matriz:

$\displaystyle C=\begin{pmatrix} 2& -1 \\[1.1ex] 3 &0\end{pmatrix}$

Calculamos la matriz simétrica y antisimétrica con las fórmulas:

$\displaystyle S=\cfrac{1}{2}\cdot (C+C^t)= \begin{pmatrix} 2& 1 \\[1.1ex] 1 &0\end{pmatrix}$

$\displaystyle A=\cfrac{1}{2}\cdot (C-C^t)= \begin{pmatrix} 0& -2 \\[1.1ex] 2 &0\end{pmatrix}$

Y podemos verificar que se cumple la ecuación sumando ambas matrices:

$\displaystyle C=S+A \quad ?$

$\displaystyle\begin{pmatrix} 2& 1 \\[1.1ex] 1 &0\end{pmatrix}+\begin{pmatrix} 0& -2 \\[1.1ex] 2 &0\end{pmatrix}=\begin{pmatrix} 2& -1 \\[1.1ex] 3 &0\end{pmatrix}$

$\displaystyle C=S+A$ ✅

Matriz simétrica