▷ ¿Qué es una matriz Ortogonal? (Ejemplos y Propiedades) ✅

En esta página podrás ver qué son las matrices ortogonales y la relación que tienen con la inversa de una matriz. También verás varios ejemplos para entenderlo perfectamente. Además, te enseñamos la fórmula que verifica toda matriz ortogonal, con lo que sabrás hallar una rápidamente. Y finalmente encontrarás las propiedades y las aplicaciones de estas peculiares matrices junto con un ejercicio resuelto típico de examen.

Sumario

1. ¿Qué es una matriz ortogonal?

2. Inversa de una matriz ortogonal

3. Ejemplo de una matriz ortogonal 2×2

4. Ejemplo de una matriz ortogonal 3×3

5. Fórmula para hallar una matriz ortogonal 2×2

6. Propiedades de la matriz ortogonal

7. Ejercicio resuelto de matrices ortogonales

8. Aplicaciones de las matrices ortogonales

¿Qué es una matriz ortogonal?

La definición de matriz ortogonal es la siguiente:

Una matriz ortogonal es una matriz cuadrada con números reales que multiplicada por su traspuesta (o transpuesta) es igual a la matriz Identidad. Es decir, se cumple la siguiente condición:

$A\cdot A^t = A^t \cdot A =I$

Donde $A$ es una matriz ortogonal y $A^t$ representa su matriz traspuesta.

Para que esta condición se cumpla, las columnas y las filas de una matriz ortogonal deben ser vectores unitarios ortogonales, o dicho de otra forma, tienen que formar una base ortonormal. Por eso mismo algunos matemáticos también las denominan matrices ortonormales.

Inversa de una matriz ortogonal

Otra manera de explicar el concepto de matriz ortogonal es mediante la matriz inversa, porque la matriz traspuesta (o transpuesta) de una matriz ortogonal es igual a su inversa.

Para comprender del todo este teorema, es importante que sepas cómo invertir una matriz. En este link encontrarás la explicación al detalle de la inversa de una matriz, todas sus propiedades e incluso tienes ejercicios resueltos paso a paso para poder practicar.

Se puede demostrar fácilmente que la matriz invertida de una matriz ortogonal es equivalente a su traspuesta mediante la condición de matriz ortogonal y la propiedad principal de las matrices inversas:

$\left.\begin{array}{c} A \cdot A^t =I \\[2ex] A \cdot A^{-1} = I\end{array} \right\} \longrightarrow \ A^t=A^{-1}$

Por lo que una matriz ortogonal siempre será una matriz invertible, o dicho de otra forma, será una matriz regular o no degenerada.

A continuación vamos a ver varios ejemplos de matrices ortogonales para acabar de entender el concepto del todo.

Ejemplo de una matriz ortogonal 2×2

La siguiente matriz es una matriz ortogonal de dimensión 2×2:

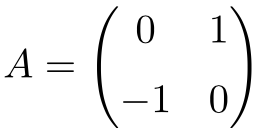
Se puede comprobar que es ortogonal calculando el producto por su traspuesta:

$\displaystyle A\cdot A^t$

$\displaystyle A\cdot A^t= \begin{pmatrix} 0 & 1 \\[1.1ex] -1 & 0 \end{pmatrix} \cdot \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}$

Como el resultado da la matriz Idéntica, se verifica que A es una matriz ortogonal.

Ejemplo de una matriz ortogonal 3×3

La siguiente matriz es una matriz ortogonal de dimensión 3×3:

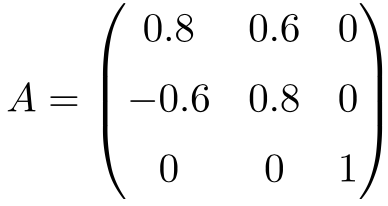
Se puede demostrar que es ortogonal multiplicando la matriz A por su traspuesta:

$\displaystyle A\cdot A^t = \begin{pmatrix}0.8&0.6&0\\[1.1ex] -0.6&0.8&0\\[1.1ex] 0&0&1\end{pmatrix}\cdot \begin{pmatrix}0.8&-0.6&0\\[1.1ex] 0.6&0.8&0\\[1.1ex] 0&0&1\end{pmatrix}= \begin{pmatrix} 1 & 0 & 0\\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0&0&1\end{pmatrix}$

Como la solución es la matriz Unidad, se demuestra que A es una matriz ortogonal.

Fórmula para hallar una matriz ortogonal 2×2

A continuación vamos a ver la demostración de que todas las matrices ortogonales de orden 2 siguen un mismo patrón.

Sea una matriz genérica de tamaño 2×2:

$\displaystyle A=\begin{pmatrix} a & b \\[1.1ex] c & d \end{pmatrix}$

Para que esta matriz sea ortogonal, se debe cumplir la siguiente ecuación matricial:

$\displaystyle A\cdot A^t =I$

$\displaystyle \begin{pmatrix} a & b \\[1.1ex] c & d \end{pmatrix} \cdot \begin{pmatrix} a & c \\[1.1ex] b & d \end{pmatrix} =\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}$

Resolviendo la multiplicación matricial, obtenemos las siguientes ecuaciones:

$\displaystyle \begin{pmatrix} a^2+b^2 & ac+bd \\[1.1ex] ac+bd & c^2+d^2 \end{pmatrix}=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}$

$\displaystyle \begin{array}{c}a^2+b^2=1 \\[2ex] ac+bd=0 \\[2ex] c^2+d^2=1 \end{array} \qquad \begin{array}{l} (1) \\[2ex] (2) \\[2ex] (3) \end{array}$

Si te fijas bien, estas igualdades son muy similares a la relación trigonométrica fundamental pitagórica:

$\displaystyle \sin ^2\alpha+\cos ^2\alpha=1$

Por lo tanto, los términos que satisfacen las ecuaciones (1) y (3) obtenidas son:

$\displaystyle \begin{array}{l} a = \cos \theta \qquad \qquad \qquad c = \sin\phi \\[2ex] b = \sin \theta \qquad \qquad \qquad d = \cos \phi\end{array}$

Además, sustituyendo los valores en la segunda ecuación obtenemos la relación entre ambos ángulos:

$\displaystyle ac+bd=0$

$\displaystyle \cos\theta\sin\phi+\sin\theta\cos\phi=0$

$\displaystyle \tan\phi=-\tan\theta$

Es decir, se debe cumplir una de las siguientes dos condiciones:

$\displaystyle \text{si} \quad c=\sin\phi=-\sin\theta \quad \longrightarrow \quad d=\cos\phi=\cos\theta$

$\displaystyle \text{si} \quad d=\cos \phi=-\cos \theta \quad \longrightarrow \quad c=\sin\phi=\sin\theta$

Por lo que, en conclusión, las matrices ortogonales deben tener la estructura de una de las siguientes dos matrices:

formula de la matriz ortogonal de dimensión 2x2

Donde $\theta$ es un número real.

De hecho, si como ejemplo otorgamos el valor $\displaystyle\theta=\frac{\pi}{2}$ y cogemos la primera estructura, obtendremos la matriz que hemos comprobado que era ortogonal en el apartado «Ejemplo de una matriz ortogonal 2×2»:

$\displaystyle M_1 \left(\theta =\frac{\pi}{2}\right)=\begin{pmatrix} \cos \cfrac{\pi}{2} &\sin \cfrac{\pi}{2} \\[4ex] -\sin \cfrac{\pi}{2} & \cos \cfrac{\pi}{2} \end{pmatrix}=\begin{pmatrix} \vphantom{\frac{\pi}{2}}0 &1 \\[2ex]\vphantom{\frac{\pi}{2}} -1 & 0 \end{pmatrix}$

Propiedades de la matriz ortogonal

Las características de este tipo de matriz son:

Una matriz ortogonal nunca puede ser una matriz singular, ya que siempre se podrá invertir. En este sentido, la inversa de una matriz ortogonal es otra matriz ortogonal.

Cualquier matriz ortogonal se puede diagonalizar. Entonces, se dice que las matrices ortogonales son diagonalizables ortogonalmente.

Todos los valores propios o autovalores de una matriz ortogonal son de módulo igual a 1.

Cualquier matriz ortogonal formada por únicamente números reales es también una matriz Normal.

El análogo de la matriz ortogonal en un entorno con números complejos es la matriz Unitaria.

Evidentemente, la matriz Identidad es una matriz ortogonal.

El conjunto de matrices ortogonales de dimensión n×n junto con la operación del producto matricial es un grupo llamado grupo ortogonal. Es decir, el producto de dos matrices ortogonales es igual a otra matriz ortogonal.

Además, el resultado de la multiplicación de una matriz ortogonal por su transpuesta se puede expresar mediante la delta de Kronecker:

$\displaystyle (A\cdot A^{t})_{ij} = \delta_{ij}=\begin{cases}1 & \mbox{si }i = j, \\[2ex] 0 & \mbox{si }i \ne j\end{cases}$

Por último, el determinante de una matriz ortogonal siempre da como resultado +1 o -1.

$\displaystyle \text{det}(A)=\pm 1$

Ejercicio resuelto de matrices ortogonales

A continuación vamos a resolver un ejercicio sobre matrices ortogonales.

Dada la siguiente matriz cuadrada de orden 3, encuentra los valores de $a$ y $b$ para que sea ortogonal:

$\displaystyle A=\frac{1}{3}\begin{pmatrix}a&a&1\\[1.1ex] b&1&b\\[1.1ex] 1&a&a\end{pmatrix}$

Para que se cumpla la ortogonalidad de la matriz, el producto de la matriz por su transpuesta debe ser igual a la matriz Identidad. Por lo tanto:

$\displaystyle A\cdot A^t = I$

$\displaystyle \frac{1}{3}\begin{pmatrix}a&a&1\\[1.1ex] b&1&b\\[1.1ex] 1&a&a\end{pmatrix} \cdot \frac{1}{3}\begin{pmatrix}a&b&1\\[1.1ex] a&1&a\\[1.1ex] 1&b&a\end{pmatrix}=\begin{pmatrix}1&0&0\\[1.1ex] 0&1&0\\[1.1ex] 0&0&1\end{pmatrix}$

Hacemos la multiplicación de las matrices:

$\displaystyle \frac{1}{9}\begin{pmatrix}2a^2+1&ab+a+b&2a+a^2\\[1.5ex] ab+a+b&2b^2+1&b+a+ab\\[1.5ex] 2a+a^2&b+a+ab&1+2a^2\end{pmatrix} =\begin{pmatrix}1&0&0\\[1.5ex] 0&1&0\\[1.5ex] 0&0&1\end{pmatrix}$

Ahora podemos conseguir una ecuación de la esquina superior izquierda de las matrices, porque los elementos situados en esa posición tienen que coincidir. Por tanto:

$\displaystyle \frac{1}{9}(2a^2+1) = 1$

Resolvemos la ecuación y despejamos la incógnita:

$\displaystyle 2a^2+1 = 9$

$\displaystyle 2a^2 = 8$

$\displaystyle a^2 = 4$

$\displaystyle \bm{a = \pm 2}$

Sin embargo, hay ecuaciones que no se cumplen con la solución positiva, por ejemplo la de la esquina superior derecha. De manera que solo es factible la solución negativa.

Por otra parte, para calcular la variable $b$ podemos igualar, por ejemplo, los términos colocados en la segunda fila de la primera columna:

$\displaystyle \frac{1}{9}(ab+a+b) = 0$

$\displaystyle ab+a+b = 0$

Sustituyendo el valor de $a$ en la ecuación:

$\displaystyle -2b-2+b = 0$

$\displaystyle -b =2$

$\displaystyle \bm{b =-2}$

En definitiva, la única solución posible es:

$\displaystyle \bm{a=b =-2}$

Por lo que la matriz ortogonal que corresponde a esos valores es:

$\displaystyle A=\frac{1}{3}\begin{pmatrix}-2&-2&1\\[1.1ex] -2&1&-2\\[1.1ex] 1&-2&-2\end{pmatrix}$

Aplicaciones de las matrices ortogonales

Aunque quizá no lo parece porque suelen tener una forma muy sencilla, las matrices ortogonales son muy importantes en matemáticas, especialmente en el campo del álgebra lineal.

En geometría, las matrices ortogonales representan transformaciones isométricas (que no modifican las distancias y los ángulos) en espacios vectoriales reales, por esa razón se llaman transformaciones ortogonales. Además, dichas transformaciones son isomorfismos internos del espacio vectorial en cuestión. Estas transformaciones pueden ser rotaciones, reflexiones especulares o inversiones.

Finalmente, este tipo de matrices también son utilizadas en la física, ya que permiten estudiar el movimiento de cuerpos rígidos. E incluso se usan en la formulación de ciertas teorías de campos.

Matriz Ortogonal