En esta página explicamos qué son las matrices antisimétricas. Además, podrás ver varios ejemplos junto con su típica estructura para entenderlo perfectamente. También explicamos qué tiene de especial el cálculo del determinante de una matriz antisimétrica y todas las propiedades de este tipo de matriz. Y, por último, encontrarás, cómo descomponer cualquier matriz cuadrada en la suma de una matriz simétrica más otra matriz antisimétrica.
¿Qué es una matriz antisimétrica?
La definición de matriz antisimétrica es la siguiente:
Una matriz antisimétrica es una matriz cuadrada cuya traspuesta es igual a la negativa de la matriz.
Donde representa la matriz transpuesta de
y
es la matriz
con todos sus elementos cambiados de signo.
Ejemplos de matrices antisimétricas
Una vez ya sabemos el concepto de matriz antisimétrica, vamos a ver varios ejemplos de matrices antisimétricas para entenderlo mejor:
Ejemplo de matriz antisimétrica de orden 2×2
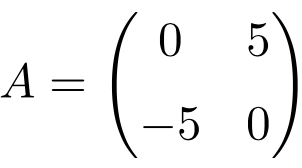
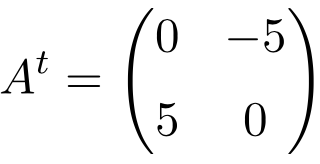
Ejemplo de matriz antisimétrica de dimensión 3×3
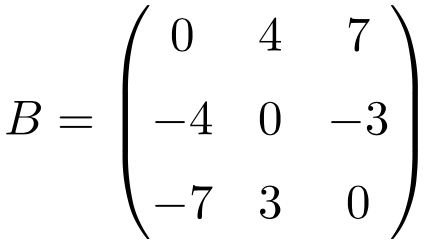
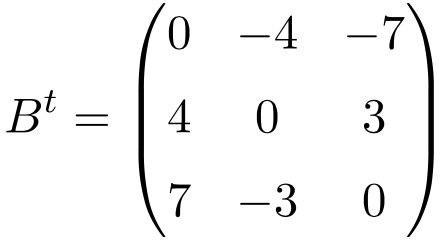
Ejemplo de matriz antisimétrica de tamaño 4×4
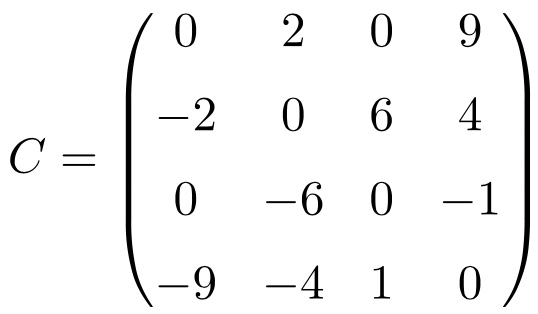
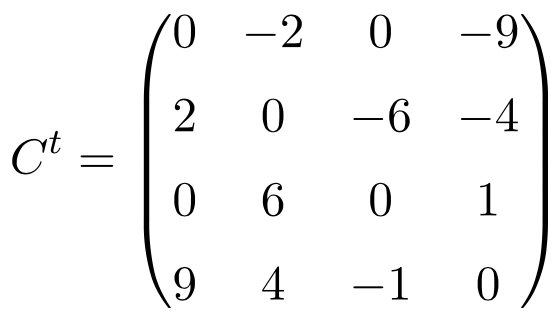
Al trasponer estas tres matrices se comprueba que son antisimétricas, porque las matrices traspuestas son equivalentes a sus respectivas matrices originales cambiadas de signo.
Estructura de una matriz antisimétrica
Para que se cumpla la condición de matriz antisimétrica, estas siempre deben tener un mismo tipo de estructura: los números de la diagonal principal son todos iguales a cero y el elemento de la fila i y la columna j es el negativo del elemento de la fila j y la columna i. Es decir, la forma de las matrices antisimétricas es la siguiente:
Por lo tanto, la diagonal principal de una matriz antisimétrica hace de eje de antisimetría. De aquí viene el nombre de esta matriz tan peculiar.
Determinante de una matriz antisimétrica
El determinante de una matriz antisimétrica depende de la dimensión de dicha matriz. Eso es debido a las propiedades de los determinantes:
De manera que si la matriz antisimétrica es de orden impar su determinante será igual a 0. En cambio, si la matriz antisimétrica es de dimensión par el determinante puede tomar cualquier valor.
Por lo tanto, una matriz antisimétrica de dimensión impar es una matriz singular o degenerada. Por contra, una matriz antisimétrica de orden par es una matriz regular.
Propiedades de las matrices antisimétricas
Las características de las matrices antisimétricas son las siguientes:
- La suma (o resta) de dos matrices antisimétricas da como resultado otra matriz antisimétrica. Ya que la transposición dos matrices sumadas (o restadas) es equivalente a transponer cada matriz por separado:
- Cualquier matriz antisimétrica multiplicada por un escalar también da lugar a otra matriz antisimétrica.
- La potencia de una matriz antisimétrica es equivalente a una matriz antisimétrica o una matriz simétrica. Si el exponente es un número par el resultado de la potencia es una matriz simétrica, pero si el exponente es un número impar el resultado de la potenciación es una matriz antisimétrica. Puedes consultar en este enlace qué es una matriz simétrica.
- La traza de una matriz antisimétrica siempre es igual a cero.
- La suma de cualquier matriz antisimétrica más la matriz unidad da lugar a una matriz invertible.
- Todos los valores propios (o autovalores) reales de una matriz antisimétrica son 0. Sin embargo, una matriz antisimétrica también puede tener valores propios complejos.
- Todas las matrices antisimétricas son matrices normales. Por lo tanto, están sujetas al teorema espectral, que dice que se puede diagonalizar una matriz antisimétrica mediante una matriz unitaria.
Descomposición de una matriz cuadrada en una matriz simétrica y otra antisimétrica
Una peculiaridad de las matrices cuadradas es que se pueden descomponer en la suma de una matriz simétrica más una matriz antisimétrica.
La fórmula que nos permite hacer esto es la siguiente:
Donde C es la matriz cuadrada que queremos descomponer, Ct su traspuesta, y finalmente S y A son las matrices simétrica y antisimiétrica respectivamente en las que se descompone la matriz C.
A continuación tienes ejercicio resuelto para demostrar la fórmula. Vamos a descomponer la siguiente matriz:
Calculamos la matriz simétrica y antisimétrica con las fórmulas:
Y podemos verificar que se cumple la ecuación sumando ambas matrices:
✅
