¿Qué es una Matriz Nilpotente? (definición, ejemplos y propiedades)

En esta página encontrarás la explicación de qué es una matriz nilpotente, así como varios ejemplos para que lo puedes entender y no te quede ninguna duda. Además, podrás ver las estructuras que tienen las matrices nilpotentes y todas las propiedades que tienen este tipos de matrices.

Sumario

1. ¿Qué es una matriz nilpotente?

2. Ejemplos de matrices nilpotentes

3. Estructura de una matriz nilpotente 2×2

4. Propiedades de las matrices nilpotentes

¿Qué es una matriz nilpotente?

La definición de matriz nilpotente es la siguiente:

Una matriz nilpotente es una matriz cuadrada que elevada a algún número entero da como resultado la matriz nula.

$N^k =0$

Donde $N$ es la matriz nilpotente y $k$ el exponente de la potencia que da como resultado la matriz nula.

Esta condición no significa que la potencia de una matriz nilpotente siempre dé cero sea cual sea el exponente, sino que si existe como mínimo una potencia de la matriz cuyo resultado es una matriz llena de 0s entonces la matriz es nilpotente.

Por otro lado, el índice de nilpotencia de una matriz nilpotente es el número más pequeño con el que se cumple la condición de nilpotencia. También se puede decir que la matriz nilpotente es de orden k, siendo k su índice de nilpotencia.

Ejemplos de matrices nilpotentes

Para acabar de entender el concepto de matriz nilpotente vamos a ver varios ejemplos de este tipo de matriz:

Ejemplo de matriz nilpotente 2×2

La siguiente matriz cuadrada de dimensión 2×2 es nilpotente:

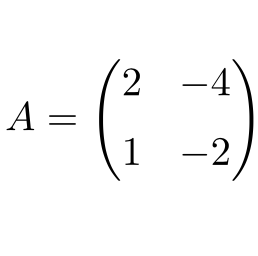
ejemplo de matriz nilpotente de dimensión 2x2

La matriz es nilpotente porque al elevar al cuadrado la matriz A obtenemos como resultado la matriz cero:

$\displaystyle A^2=\begin{pmatrix} 2 &-4 \\[1.1ex] 1 & -2 \end{pmatrix}\cdot \begin{pmatrix} 2 &-4 \\[1.1ex] 1 & -2 \end{pmatrix}=\begin{pmatrix} \bm{0} &\bm{0} \\[1.1ex] \bm{0} & \bm{0} \end{pmatrix}$

Por lo tanto, se trata de una matriz nilpotente y su índice de nilpotencia es 2, ya que la matriz nula se obtiene con la segunda potencia.

Ejemplo de matriz nilpotente 3×3

La siguiente matriz cuadrada de orden 3 es nilpotente:

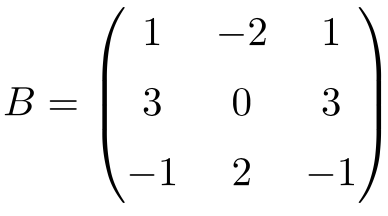
ejemplo de matriz nilpotente de dimensión 3x3

Aunque al elevar la matriz a la 2 no obtenemos la matriz nula:

$\displaystyle B^2=\begin{pmatrix}1&-2&1\\[1.1ex] 3&0&3\\[1.1ex] -1&2&-1\end{pmatrix}\cdot \begin{pmatrix}1&-2&1\\[1.1ex] 3&0&3\\[1.1ex] -1&2&-1\end{pmatrix}= \begin{pmatrix}-6&0&-6\\[1.1ex]0&0&0\\[1.1ex] 6&0&6\end{pmatrix}$

Pero al calcular el cubo de la matriz sí que conseguimos una matriz con todos los elementos igual a 0:

$\displaystyle B^3= \begin{pmatrix}-6&0&-6\\[1.1ex]0&0&0\\[1.1ex] 6&0&6\end{pmatrix}\cdot\begin{pmatrix}1&-2&1\\[1.1ex] 3&0&3\\[1.1ex] -1&2&-1\end{pmatrix}= \begin{pmatrix}\bm{0}&\bm{0}&\bm{0}\\[1.1ex]\bm{0}&\bm{0}&\bm{0}\\[1.1ex] \bm{0}&\bm{0}&\bm{0}\end{pmatrix}$

De manera que la matriz B es una matriz nilpotente, y como la matriz nula se obtiene con la tercera potencia su índice de nilpotencia es 3.

Estructura de una matriz nilpotente 2×2

A continuación puedes ver la estructura que tienen todas las matrices nilpotentes. Su demostración es un poco tediosa, así que te hemos dejado directamente la fórmula para obtener una matriz nilpotente de orden 2:

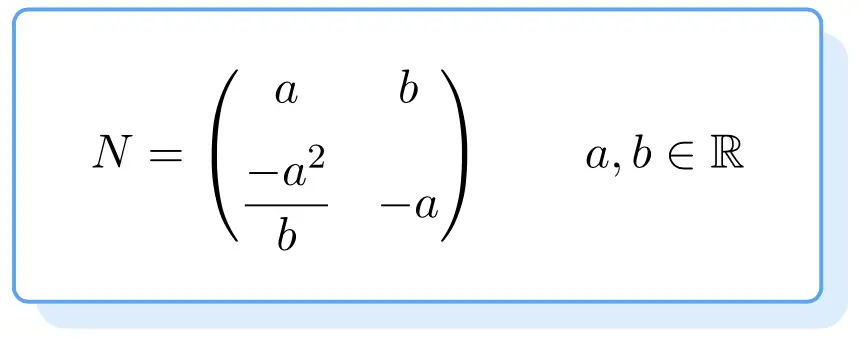
estructura y formula de una matriz nilpotente 2x2

De modo que cualquier matriz que verifique la fórmula anterior será una matriz nilpotente. Para ello, los valores $a$ y $b$ pueden ser cualesquiera mientras sean números reales.

Propiedades de las matrices nilpotentes

Las matrices nilpotentes tienen las siguientes características:

La traza de una matriz nilpotente siempre es cero.

Del mismo modo, el determinante de cualquier matriz nilpotente siempre es igual a 0. Sin embargo, el recíproco no es cierto, es decir, que el determinante de una matriz sea cero no implica que la matriz sea nilpotente.

La única matriz nilpotente diagonalizable es la matriz nula.

El índice de nilpotencia de una matriz nilpotente de dimensión n×n siempre es igual o menor a n. Por eso el índice de nilpotencia de una matriz nilpotente 2×2 siempre será 2.

Una matriz nilpotente no es invertible.

Cualquier matriz triangular con ceros en la diagonal principal también es una matriz nilpotente a la vez.

Existe un teorema que dice que si la matriz $N$ es nilpotente, entonces la matriz $N+I$ es invertible, donde $I$ es la matriz Identidad. Además, su matriz inversa se puede hallar con la siguiente fórmula:

$\displaystyle(N+I)^{-1} = \sum_{m = 0}^\infty (-N)^m=I-N+N^2-N^3+\cdots$

De forma equivalente, si $N$ es una matriz nilpotente, entonces se puede calcular la inversa de la matriz $N-I$ con la siguiente ecuación:

$\displaystyle(N-I)^{-1} = \sum_{m = 0}^\infty (N)^m=I+N+N^2+N^3+\cdots$

Toda matriz singular, es decir que no se puede invertir, se puede descomponer en el producto de matrices nilpotentes.

Todos los valores propios (o autovalores) de una matriz nilpotente son cero.

$\displaystyle \lambda=0 \qquad \forall \ \lambda$

Finalmente, como curiosidad, también existe el concepto de transformación nilpotente, que define una aplicación lineal $L$ de un espacio vectorial tal que $L^k=0$ .

Matriz nilpotente