▷ Matriz triangular (superior e inferior): ejemplos, propiedades,...

En esta página podrás ver qué es una matriz triangular y los diferentes tipos de matrices triangulares que hay junto con ejemplos. Además, encontrarás cómo calcular el determinante de una matriz triangular y cuáles son las propiedades de esta matriz tan interesante. Finalmente, también explicamos qué es una matriz de Hessenberg, ya que es una matriz que está relacionada con las matrices triangulares.

Sumario

1. ¿Qué es una matriz triangular?

2. Matriz triangular superior

3. Matriz triangular inferior

4. Ejemplos de matrices triangulares

5. Determinante de una matriz triangular

6. Propiedades de la matriz triangular

7. Triangularizar una matriz

8. Matriz de Hessenberg

¿Qué es una matriz triangular?

Definición de matriz triangular:

Una matriz triangular es una matriz cuadrada en la que todos los elementos por encima o por debajo de diagonal principal son cero (0).

Las matrices triangulares se utilizan mucho en cálculos de álgebra lineal, porque invertir una matriz triangular, calcular su determinante o incluso resolver sistemas de ecuaciones lineales con este tipo de matrices es mucho más fácil que con matrices que tienen elementos diferentes de 0 en todas las posiciones.

Matriz triangular superior

Una matriz triangular superior es una matriz cuadrada cuyos elementos por debajo de la diagonal principal son cero (0).

Ejemplo de matriz triangular superior:

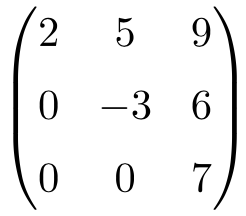
Matriz triangular inferior

Una matriz triangular inferior es aquella matriz cuadrada que tiene un cero (0) en cada elemento que está por encima de la diagonal principal.

Ejemplo de matriz triangular inferior:

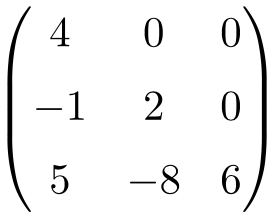
A veces también se llama a estas matrices con la letra U, para la matriz triangular superior, y con la letra L, para la matriz triangular inferior. Aunque esta nomenclatura se utiliza sobre todo en inglés, de hecho, la U viene de upper triangular matrix y la L de lower triangular matrix.

Ejemplos de matrices triangulares

Matriz triangular de dimensión 2×2

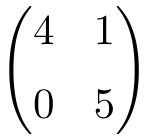
Matriz triangular de orden 3×3

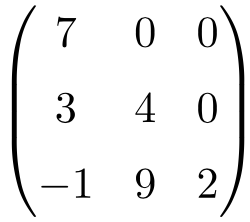
Matriz triangular de tamaño 4×4

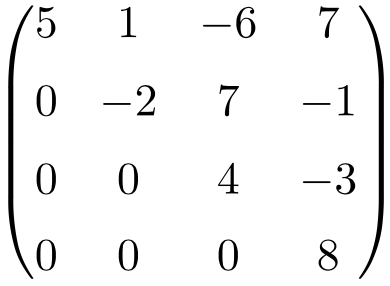
Determinante de una matriz triangular

El determinante de una matriz triangular, sea triangular superior o inferior, es el producto de los elementos de la diagonal principal.

Fíjate en el siguiente ejercicio resuelto como simplemente se tiene que calcular la multiplicación de los elementos de la diagonal principal de la matriz triangular para hallar su determinante:

$\displaystyle \begin{vmatrix} 2 & 5 & -6 \\[1.1ex] 0 & 4 & 9 \\[1.1ex] 0 & 0 & 3 \end{vmatrix} = 2 \cdot 4 \cdot 3 = \bm{24}$

Este teorema se puede demostrar fácilmente: solo tenemos que calcular el determinante de una matriz triangular por bloques (o cofactores). A continuación se detalla esta demostración mediante una matriz triangular genérica:

$\begin{aligned} \begin{vmatrix} a & b & c \\[1.1ex] 0 & d & e \\[1.1ex] 0 & 0 & f \end{vmatrix}& = a \cdot \begin{vmatrix} d & e \\[1.1ex] 0 & f \end{vmatrix} - b \cdot \begin{vmatrix} 0 & e \\[1.1ex] 0 & f \end{vmatrix} + c \cdot \begin{vmatrix} 0 & d \\[1.1ex] 0 & 0 \end{vmatrix} \\[2ex] & =a \cdot (d\cdot f) - b \cdot 0 + c \cdot 0 \\[2ex] & = a \cdot d \cdot f \end{aligned}$

Por otro lado, sabemos que una matriz es invertible si su determinante es diferente de 0. Por lo tanto, si ningún elemento de la diagonal principal es 0 la matriz triangular también será invertible y, en consecuencia, será una matriz regular.

Propiedades de la matriz triangular

Veamos ahora cuáles son las propiedades de las matrices triangulares:

El producto de dos matrices triangulares superiores es igual a una matriz triangular superior. Y al revés: multiplicar dos matrices triangulares inferiores da como resultado otra matriz triangular inferior.

$\begin{pmatrix} 3 & 1 & 4 \\[1.1ex] 0 & -1 & 2 \\[1.1ex] 0 & 0 & 5 \end{pmatrix} \cdot \begin{pmatrix} 6 & 2 & 1 \\[1.1ex] 0 & 3 & 5 \\[1.1ex] 0 & 0 & 9 \end{pmatrix} = \begin{pmatrix}18&9&44\\[1.1ex] 0&-3&13\\[1.1ex]0&0&45\end{pmatrix}$

La transpuesta de una matriz triangular superior es una matriz triangular inferior, y viceversa: la traspuesta de una matriz triangular inferior es una matriz triangular superior.

$\left.\begin{pmatrix} 1 & 2 & 6 & 3 \\[1.1ex] 0 & 9 & 4 & 1 \\[1.1ex] 0 & 0 & -2 & 8 \\[1.1ex] 0 & 0 & 0 & 7 \end{pmatrix}\right.^{\bm{t}} = \begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex] 2 & 9 & 0 & 0 \\[1.1ex] 6 & 4 & -2 & 0 \\[1.1ex] 3 & 1 & 8 & 7 \end{pmatrix}$

Una matriz triangular es invertible si todos sus elementos de la diagonal principal son no nulos, es decir, si son diferente de cero. En tal caso, la inversa de una matriz triangular superior (inferior) también es una matriz triangular superior (inferior).

$\left. \begin{pmatrix}1&0&0\\[1.1ex] -3&2&0\\[1.1ex] 2&4&3\end{pmatrix} \right.^{-1} =\begin{pmatrix}1&0&0\\[1.1ex] \frac{3}{2}&\frac{1}{2}&0\\[1.1ex] -\frac{8}{3}&-\frac{2}{3}&\frac{1}{3}\end{pmatrix}$

Además, la diagonal principal de la matriz invertida siempre contendrá los inversos de los elementos de la diagonal principal de la matriz triangular original.

Cualquier matriz diagonal es una matriz triangular superior y triangular inferior a la vez, por ejemplo:

$\begin{pmatrix} 3 & 0 & 0 \\[1.1ex] 0 & 8 & 0 \\[1.1ex] 0 & 0 & -2 \end{pmatrix}$

Por tanto, una matriz escalar también es una matriz triangular superior e inferior. Por ejemplo la matriz identidad:

$\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

Evidentemente, la matriz nula también es una matriz triangular superior e inferior, porque los elementos por encima y por debajo de la diagonal principal son 0:

$\begin{pmatrix} 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \end{pmatrix}$

Los valores propios (o autovalores) de una matriz triangular son los elementos de la diagonal principal.

$\begin{pmatrix} 5 & 0 & 0 \\[1.1ex] 1 & 3 & 0 \\[1.1ex] 2 & 6 & -2 \end{pmatrix} \longrightarrow \ \lambda = -2 \ ; \ \lambda = 3 \ ; \ \lambda = 5$

Una matriz triangular superior o inferior siempre es capaz de diagonalizar en una base de vectores propios (o autovectores).

Cualquier matriz puede ser factorizada en el producto de una matriz triangular inferior por una matriz triangular superior. Es decir, cualquier matriz se puede transformar en una multiplicación de matrices triangulares. Además, si la matriz es invertible esta transformación es única. Para factorizar una matriz se suele utilizar el método de descomposición LU.

Triangularizar una matriz

Existen varios teoremas acerca de matrices triangularizables mediante cambios de bases. Sin embargo, aquí vamos a ver cómo triangularizar una matriz aplicando transformaciones elementales en las filas, como en el método de Gauss.

Por ejemplo:

$\begin{pmatrix} 1 & 2 & 4 \\[1.1ex] 2 & -3 & 5 \\[1.1ex]1 & -1 & 6 \end{pmatrix} \begin{array}{c} \\[1.1ex] \xrightarrow{f_2 -2f_1}\\[1.1ex] \xrightarrow{f_3 -f_1} \end{array} \begin{pmatrix} 1 & 2 & 4 \\[1.1ex] 0 & -7 & -3 \\[1.1ex] 0 & -3 & 2 \end{pmatrix}\begin{array}{c} \\[1.1ex]\\[1.1ex] \xrightarrow{7f_3 -3f_2} \end{array} \begin{pmatrix} 1 & 2 & 4 \\[1.1ex] 0 & -7 & -3 \\[1.1ex] 0 & 0 & 23 \end{pmatrix}$

Y de esta forma ya hemos triangularizado la matriz original.

Recuerda que las transformaciones elementales permitidas entre filas en el método de Gauss son:

Sustituir una fila por la combinación lineal de otras filas.
Multiplicar o dividir todos los términos de una fila por un número diferente de 0.
Cambiar las filas de orden.

Matriz de Hessenberg

La definición de la matriz de Hessenberg es la siguiente:

La matriz de Hessenberg es una matriz «casi» triangular, es decir, todos sus elementos son cero a partir de la primera subdiagonal (matriz de Hessenberg superior) o a partir de la primera superdiagonal (matriz de Hessenberg inferior).

Seguro que se entiende mejor con un ejemplo de una matriz de Hessenberg superior y otro ejemplo de una matriz de Hessenberg inferior:

Matriz de Hessenberg Superior

$\left.\begin{pmatrix} 3 & 5 & 1 & 4 \\[1.1ex] 8 & 2 & 7 & 1 \\[1.1ex] 0 & 6 & 3 & 5 \\[1.1ex] 0 & 0 & 1 & 9 \end{pmatrix}$

Matriz de Hessenberg Inferior

$\left.\begin{pmatrix} 2 & 4 & 0 & 0 \\[1.1ex] 1 & 9 & 6 & 0 \\[1.1ex] 3 & 5 & 1 & 2 \\[1.1ex] 8 & 2 & 3 & 7 \end{pmatrix}$

Una matriz que es una matriz de Hessenberg superior e inferior a la vez es una matriz tridiagonal.

Esta matriz fue llamada así en honor a Karl Hessenberg, un importante ingeniero y matemático alemán del siglo XX.

Por último, este tipo de matriz tiene la característica de que si se multiplica por una matriz triangular, el resultado sigue siendo una matriz de Hessenberg.

Matriz triangular superior e inferior