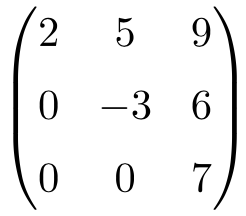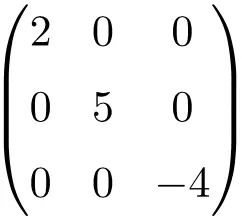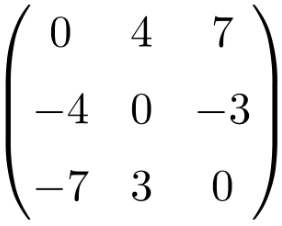En esta página te explicamos qué es un matriz cuadrada y encontrarás ejemplos de matrices cuadradas. Además, verás cuáles son las propiedades de las matrices cuadradas, las operaciones que se pueden hacer con ellas y los diferentes tipos que existen.
¿Qué es una matriz cuadrada?
Una matriz cuadrada es una matriz que tiene el mismo número de filas que de columnas.
Ejemplos de matrices cuadradas
Matriz cuadrada de orden 2
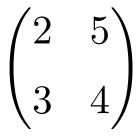
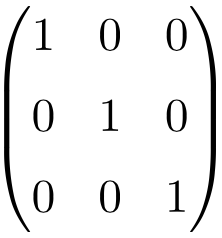
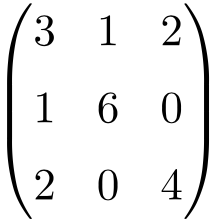
Matriz cuadrada de orden 3
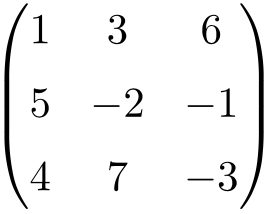
Matriz cuadrada de orden 4
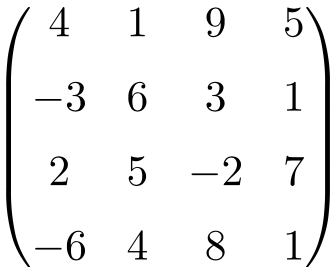
Como ves, las matrices cuadradas se suelen nombrar por su orden, es decir, una matriz cuadrada de orden 2 significa que es una matriz de dimensión 2×2 (2 filas y 2 columnas), o cuando hablamos de una matriz cuadrada de orden 3 se está indicando que es de tamaño 3×3 (3 filas y 3 columnas).
Diagonales de una matriz cuadrada
Las diagonales de las matrices cuadradas tienen nombres especiales, existe la diagonal principal y la diagonal secundaria:
- La diagonal principal de una matriz cuadrada son los elementos que van desde la esquina superior izquierda hasta la esquina inferior derecha:
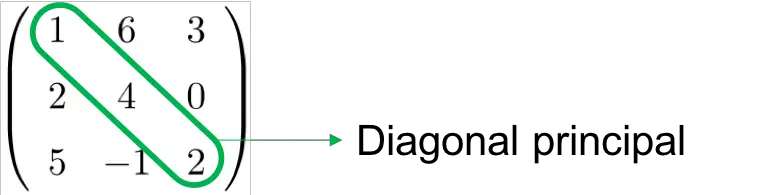
- La diagonal secundaria de una matriz cuadrada son los elementos que van desde la esquina inferior izquierda hasta la esquina superior derecha:
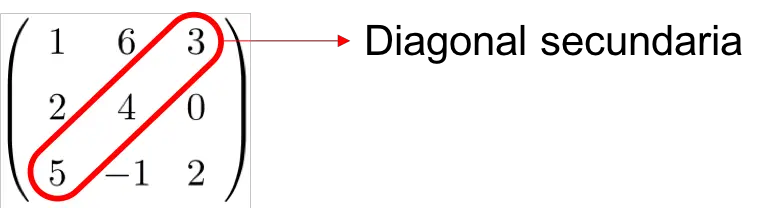
Propiedades de una matriz cuadrada
Las matrices cuadradas se utilizan mucho en álgebra lineal, por eso son tan importantes. Así que vamos a ver cuáles son las características que hacen que esta clase de matrices sean tan relevantes:
- Cualquier matriz cuadrada se puede descomponer en una suma de una matriz simétrica y una matriz antisimétrica.
- Si dos matrices cuadradas son del mismo orden, se pueden sumar o restar entre sí:
- Se pueden multiplicar dos matrices cuadradas en los dos sentidos posibles. Sin embargo, el producto de matrices cuadradas no es conmutativo, es decir, el resultado de la multiplicación cambiará según el lado por el que se multiplique. Fíjate en el siguiente ejemplo como el resultado depende de las posiciones de las matrices:
- Las matrices cuadradas son las únicas que permiten calcular el determinante. Por lo tanto, solo se puede resolver un determinante si se trata de una matriz cuadrada. Por ejemplo, para hallar el determinante de una matriz cuadrada 3×3 se tiene que aplicar la Regla de Sarrus:
Además, recuerda que si el determinante de la matriz es diferente de 0 significa que es una matriz regular, es decir, que es invertible. Por contra, si el determinante es nulo, se trata de una matriz singular (que no tiene inversa).
- Por último, las matrices cuadradas se pueden diagonalizar. De manera que se puede hacer un cambio de base para calcular los valores propios (o autovalores) y los vectores propios (o autovectores) de una matriz cuadrada.
Operaciones con matrices cuadradas
Como hemos visto, el determinante de una matriz solo se puede calcular si la matriz es cuadrada. Del mismo modo, también hay determinadas operaciones que únicamente se pueden realizar si la matriz es de dimensión cuadrada:
Traza de una matriz
La traza de una matriz es la suma de los elementos que forman la diagonal principal de una matriz cuadrada.
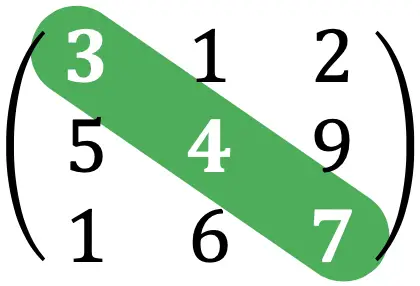
Por ejemplo, la traza de la matriz del ejercicio de arriba sería:
Tipos de matrices cuadradas
A continuación tienes los tipos de matrices cuadradas más importantes que existen. Haz clic en el tipo de matriz para saber qué tiene de especial.
Como ves hay muchos tipos de matrices cuadradas, y cada una tiene su propio nombre por una distinta razón.