¿Qué es una Matriz Escalar? (definición, ejemplos y propiedades)

En esta página encontrarás qué es una matriz escalar y varios ejemplos de matrices escalares para que se entienda perfectamente. Además, podrás ver todas las propiedades de las matrices escalares y las ventajas que tiene hacer operaciones con ellas. Finalmente, explicamos cómo calcular el determinante de una matriz escalar y cómo invertir este tipo de matriz.

Sumario

1. ¿Qué es una matriz escalar?

2. Ejemplos de matrices escalares

3. Propiedades de las matrices escalares

4. Operaciones con matrices escalares

4.1. Suma y resta de matrices escalares

4.2. Multiplicación de matrices escalares

4.3. Potencia de matrices escalares

5. Determinante de una matriz escalar

6. Invertir una matriz escalar

¿Qué es una matriz escalar?

Una matriz escalar es una matriz diagonal en la que todos los valores de la diagonal principal son iguales.

Esta es la definición de una matriz escalar, pero seguro que se entiende mejor con ejemplos: 😉

Ejemplos de matrices escalares

Ejemplo de matriz escalar de orden 2×2

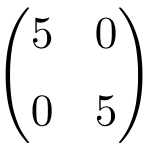
ejemplo de matriz escalar de dimensión 2x2

Ejemplo de matriz escalar de dimensión 3×3

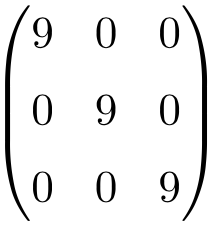
ejemplo de matriz escalar de dimensión 3x3

Ejemplo de matriz escalar de tamaño 4×4

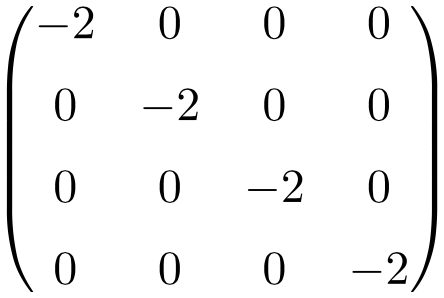
ejemplo de matriz escalar de dimensión 4x4

Propiedades de las matrices escalares

La matriz escalar es al mismo tiempo una matriz diagonal, por eso verás que hereda muchas características de esta clase de matriz:

Todas las matrices escalares también son matrices simetricas.

Una matriz escalar es una matriz triangular superior y matriz triangular inferior a la vez.

La matriz identidad se trata de una matriz escalar.

Cualquier matriz escalar se puede obtener del producto de una matriz identidad por un número escalar.

$4 \cdot \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 4 & 0 & 0 \\[1.1ex] 0 & 4 & 0 \\[1.1ex] 0 & 0 & 4 \end{pmatrix}$

La matriz nula también es una matriz escalar.

Los valores propios (o autovalores) de una matriz escalar son los elementos de su diagonal principal. Por lo tanto, sus valores propios siempre serán iguales y estarán repetidos tantas veces como la dimensión de la matriz.

$\begin{pmatrix} 8 & 0 & 0 \\[1.1ex] 0 & 8 & 0 \\[1.1ex] 0 & 0 & 8 \end{pmatrix} \longrightarrow \ \lambda = 8 \ ; \ \lambda = 8 \ ; \ \lambda = 8$

La adjunta de una matriz escalar es otra matriz escalar. Y, además, los valores de la diagonal principal de la matriz adjunta siempre serán los de la matriz original elevados al orden de la matriz – 1.

$\displaystyle A=\begin{pmatrix} 5 & 0 & 0 \\[1.1ex] 0 & 5 & 0 \\[1.1ex] 0 & 0 & 5 \end{pmatrix} \longrightarrow \text{Adj}(A)=\begin{pmatrix} 5^{3-1} & 0 & 0 \\[1.1ex] 0 & 5^{3-1} & 0 \\[1.1ex] 0 & 0 & 5^{3-1} \end{pmatrix}= \begin{pmatrix} 25 & 0 & 0 \\[1.1ex] 0 & 25 & 0 \\[1.1ex] 0 & 0 & 25 \end{pmatrix}$

Operaciones con matrices escalares

Una de las razones por las que las matrices escalares son tan utilizadas en el álgebra lineal es la facilidad con la que permiten realizar cálculos. Por eso son tan importantes en las matemáticas.

Veamos pues por qué resulta tan fácil hacer cálculos con este tipo de matrices cuadradas:

Suma y resta de matrices escalares

La suma (y la resta) de dos matrices escalares es muy simple: simplemente hay que sumar (o restar) los números de las diagonales principales. Por ejemplo:

$\displaystyle \begin{pmatrix} 4 & 0 & 0 \\[1.1ex] 0 & 4 & 0 \\[1.1ex] 0 & 0 & 4 \end{pmatrix} +\begin{pmatrix} 3 & 0 & 0 \\[1.1ex] 0 & 3 & 0 \\[1.1ex] 0 & 0 & 3 \end{pmatrix} = \begin{pmatrix} 7& 0 & 0 \\[1.1ex] 0 & 7 & 0 \\[1.1ex] 0 & 0 & 7 \end{pmatrix}$

Multiplicación de matrices escalares

De manera similar a la suma y la resta, para resolver una multiplicación o un producto matricial entre dos matrices escalares únicamente hay que multiplicar los elementos de las diagonales entre sí. Por ejemplo:

$\displaystyle \begin{pmatrix} 2 & 0 & 0 \\[1.1ex] 0 & 2 & 0 \\[1.1ex] 0 & 0 & 2 \end{pmatrix} \cdot\begin{pmatrix} 6 & 0 & 0 \\[1.1ex] 0 & 6 & 0 \\[1.1ex] 0 & 0 & 6 \end{pmatrix} = \begin{pmatrix} 12 & 0 & 0 \\[1.1ex] 0 & 12 & 0 \\[1.1ex] 0 & 0 & 12 \end{pmatrix}$

Potencia de matrices escalares

El cálculo de la potencia de una matriz escalar también es muy fácil: tenemos que elevar cada elemento de la diagonal al exponente. Por ejemplo:

$\displaystyle\left. \begin{pmatrix} 2 & 0 & 0 \\[1.1ex] 0 & 2 & 0 \\[1.1ex] 0 & 0 & 2 \end{pmatrix}\right.^4=\begin{pmatrix} 2^4 & 0 & 0 \\[1.1ex] 0 & 2^$ & 0 \\[1.1ex] 0 & 0 & 2^4 \end{pmatrix}= \begin{pmatrix} 16 & 0 & 0 \\[1.1ex] 0 & 16 & 0 \\[1.1ex] 0 & 0 & 16 \end{pmatrix}$

Determinante de una matriz escalar

Calcular el determinante de una matriz escalar es igual que resolver el determinante de una matriz diagonal: el resultado es el producto de los elementos de la diagonal principal.

$\displaystyle \text{det}(A)= \prod_{i =1}^n a_i$

Fíjate en el siguiente ejercicio resuelto en el que hallamos el determinante de una matriz escalar multiplicando los elementos de su diagonal principal:

$\displaystyle \begin{vmatrix} 7 & 0 & 0 \\[1.1ex] 0 & 7 & 0 \\[1.1ex] 0 & 0 & 7 \end{vmatrix} = 7 \cdot 7 \cdot 7 = \bm{343}$

De hecho, como todos los elementos de la diagonal principal de una matriz escalar siempre son iguales, para hallar el resultado del determinante solamente tenemos que elevar el número de la diagonal principal por el número de veces que está repetido. Por lo tanto, el ejercicio anterior también se puede solucionar de la siguiente forma:

$\displaystyle \begin{vmatrix} 7 & 0 & 0 \\[1.1ex] 0 & 7 & 0 \\[1.1ex] 0 & 0 & 7 \end{vmatrix} = 7^3= \bm{343}$

Demostrar este teorema es muy sencillo: únicamente tenemos que calcular el determinante de una matriz escalar por bloques (o cofactores). A continuación se detalla la demostración de la fórmula mediante una matriz escalar genérica:

$\begin{aligned} \begin{vmatrix} a & 0 & 0 \\[1.1ex] 0 & a & 0 \\[1.1ex] 0 & 0 & a \end{vmatrix}& = a \cdot \begin{vmatrix} a & 0 \\[1.1ex] 0 & a \end{vmatrix} - 0 \cdot \begin{vmatrix} 0 & 0 \\[1.1ex] 0 & a \end{vmatrix} + 0 \cdot \begin{vmatrix} 0 & a \\[1.1ex] 0 & 0 \end{vmatrix} \\[2ex] & =a \cdot (a\cdot a) - 0 \cdot 0 + 0 \cdot 0 \\[2ex] & = a \cdot a \cdot a \\[2ex] & = a^3 \end{aligned}$

En este caso da $a^3$ porque la matriz es de orden 3, pero siempre debemos elevarlo al orden de la matriz.

Invertir una matriz escalar

Una matriz escalar es invertible si, y solo si, todos los elementos de la diagonal principal son diferentes de 0. En dicho caso decimos que la matriz escalar es una matriz regular.

Además, la inversa de una matriz escalar siempre será otra matriz escalar con los inversos de la diagonal principal:

$\displaystyle A= \begin{pmatrix} 9 & 0 & 0 \\[1.1ex] 0 & 9 & 0 \\[1.1ex] 0 & 0 & 9 \end{pmatrix} \ \longrightarrow \ A^{-1}=\begin{pmatrix} \frac{1}{9} & 0 & 0 \\[1.1ex] 0 & \frac{1}{9} & 0 \\[1.1ex] 0 & 0 & \frac{1}{9} \end{pmatrix}$

Por otro lado, a partir de la característica anterior se puede deducir que el determinante de una matriz escalar invertida es el resultado de multiplicar los inversos de la diagonal principal:

$\displaystyle B= \begin{pmatrix} 2 & 0 & 0 \\[1.1ex] 0 & 2 & 0 \\[1.1ex] 0 & 0 & 2 \end{pmatrix}$

$\displaystyle\left| B^{-1}\right|=\cfrac{1}{2} \cdot \cfrac{1}{2} \cdot \cfrac{1}{2}=\cfrac{1}{8} = 0,125$

3 comentarios en “Matriz escalar”

Jose gregorio
25/05/2021 a las 19:25

Bueno gracias i Dios le bendiga

Responder
Carlos
13/11/2021 a las 22:16

gracias pero me surgio una duda en la definición que decía :
«Una matriz escalar es una matriz diagonal en la que todos los valores de la diagonal principal son iguales. »
pero en todos los ejemplos los demás elementos fuera de la diagonal principal eran cero como
/ 2 0 0 \ / 2 2 2 \
B=| 0 2 0 | entonces que pasa si tuviéramos una matriz X=| 2 2 2 |
\ 0 0 2 / \ 2 2 2 /
¿seria una matriz diagonal? porque todos los elementos de su diagonal principal son iguales,
o una matriz diagonal ademas de que todos sus elementos sean iguales en su diagonal principal debe tener todos sus elementos igual a cero fuera de la diagonal principal.
Le agradeceria su respuesta

Responder
1. Matrices y Determinantes
  15/11/2021 a las 15:31
  
  Hola Carlos,
  
  Efectivamente, una matriz solo se considera matriz diagonal si todos sus elementos que no están en la diagonal principal son ceros (puede haber algún cero en la diagonal principal también). Por lo tanto, para que una matriz sea escalar debe tener todos los elementos de la diagonal principal iguales, y el resto de sus números deben ser ceros.
  
  Si estás interesado, puedes consultar nuestro post sobre las matrices diagonales donde se explica detalladamente este tipo de matriz.
  
  Responder