Matrices conmutables

En esta página explicamos qué son las matrices conmutables. Además, podrás ver ejemplos para entender perfectamente el concepto y, finalmente, encontrarás un ejercicio resuelto paso a paso en el que enseñamos a calcular todas las matrices que conmutan con cualquier matriz.

Sumario
1. ¿Qué son las matrices conmutables?
2. Ejemplo de matrices conmutables
3. Ejercicio resuelto de conmutar matrices
4. Propiedades de las matrices conmutables

¿Qué son las matrices conmutables?

Dos matrices son conmutables si el resultado de su producto no depende del orden de multiplicación. Es decir, las matrices conmutables cumplen la siguiente condición:

\displaystyle A\cdot B = B \cdot A

Esta es la definición de matrices conmutables, veamos ahora un ejemplo:

Ejemplo de matrices conmutables

Las siguientes dos matrices de dimensión 2×2 son conmutables entre sí:

\displaystyle A=\begin{pmatrix} 2 & 0\\[1.1ex] 1 & -1 \end{pmatrix} \quad B= \begin{pmatrix} 3& 0\\[1.1ex] 1 & 0\end{pmatrix}

Se pude demostrar la conmutabilidad de las dos matrices calculando su producto en ambos sentidos:

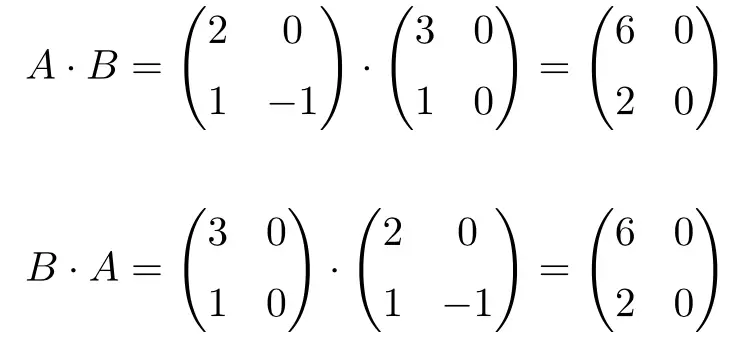
ejemplo de matrices conmutables de dimensión 2x2

Como puedes ver, el resultado de las dos multiplicaciones es igual, independientemente del orden en el que se multiplican. Por lo tanto, las matrices A y B son conmutables.

Ejercicio resuelto de conmutar matrices

A continuación vamos a ver paso a paso cómo se resuelve un ejercicio de matrices conmutables:

  • Determina todas las matrices que conmutan con la siguiente matriz cuadrada:

\displaystyle A=\begin{pmatrix} 3 & 1\\[1.1ex] 1 & 0 \end{pmatrix}

Para resolver este problema crearemos una matriz incógnita:

\displaystyle B=\begin{pmatrix} a & b\\[1.1ex] c & d \end{pmatrix}

De manera que debemos hallar esta matriz incógnita.

Para ello, nos aprovecharemos de la propiedad que cumplen todas las matrices que conmutan:

\displaystyle A\cdot B = B \cdot A

\displaystyle \begin{pmatrix}3 & 1\\[1.1ex] 1 & 0\end{pmatrix}\cdot \begin{pmatrix} a & b\\[1.1ex] c & d \end{pmatrix} = \begin{pmatrix} a & b\\[1.1ex] c & d \end{pmatrix} \cdot \begin{pmatrix} 3 & 1\\[1.1ex] 1 & 0 \end{pmatrix}

Ahora multiplicamos las matrices en los dos miembros de la ecuación:

\displaystyle \begin{pmatrix} 3a+c &3b+d\\[1.1ex] a & b \end{pmatrix} = \begin{pmatrix}3a+b & a\\[1.1ex] 3c+d & c \end{pmatrix}

Por lo tanto, para que se cumpla la igualdad se tienen que cumplir las siguientes ecuaciones:

\left.\begin{array}{l} 3a+c=3a+b \\[2ex] 3b+d=a \\[2ex] a=3c+d\\[2ex] b= c \end{array}\right\}

De modo que ahora solo debemos resolver el sistema de ecuaciones. De la última ecuación podemos deducir que b tiene que ser igual a c:

b=c

Y si estas dos incógnitas son equivalentes la tercera ecuación está repetida con la segunda, así que la podemos eliminar:

\left.\begin{array}{l} 3a+c=3a+b \\[2ex] 3b+d=a \\[2ex] \cancel{a=3c+d}\\[2ex] b= c \end{array}\right\}

Además, de la primera ecuación no podemos sacar ninguna conclusión, porque:

3a+c=3a+b \ \xrightarrow{b \ = \ c} \ 3a+b=3a+b  

3a=3a

a=a

Por tanto, solo nos quedan la segunda y la última ecuación:

\left.\begin{array}{l} 3b+d=a \\[2ex] b= c \end{array}\right\}

De manera que las matrices que conmutan con la matriz A son todas aquellas que verifican las dos ecuaciones anteriores. Por tanto, sustituyendo las expresiones encontradas en la matriz incógnita del principio podemos encontrar la forma de las matrices que conmutan con A:

\displaystyle \begin{pmatrix} a & b\\[1.1ex] c & d \end{pmatrix} \ \longrightarrow \ \begin{pmatrix} 3b+d & b \\[1.1ex] b & d \end{pmatrix}

Donde b y d son dos números reales.

Así que un ejemplo de una matriz que conmutaría con la matriz A sería la siguiente:

\displaystyle \begin{pmatrix} 6 & 1 \\[1.1ex] 1 & 3 \end{pmatrix}

Propiedades de las matrices conmutables

Las matrices conmutables tienen las siguientes características:

  • Las matrices conmutables no poseen la propiedad transitiva. Es decir, aunque la matriz A conmute con las matrices B y C, esto no significa que B y C sean conmutables entre sí.
  • Las matrices diagonales conmutan entre sí, es decir, una matriz diagonal conmuta con cualquier otra matriz diagonal.
  • Del mismo modo, una matriz escalar también conmuta con todas las matrices. Por ejemplo, la matriz Identidad o Unidad conmuta con todas las matrices.
  • Evidentemente, la matriz cero también conmuta con todas las matrices.
  • Si el producto de dos matrices simétricas da como resultado otra matriz simétrica, entonces las dos matrices tienen que conmutar.
  • Si la diagonalización de dos matrices se puede hacer de forma simultánea, estas tienen que ser conmutables. Por lo tanto, estas dos matrices también comparten la misma base ortonormal de vectores propios o autovectores.

7 comentarios en “Matrices conmutables”

  1. Manuel García

    Soy estudiante del primer año de ingeniería en Buenos Aires, este material es para mí muy útil y didáctico. Les quedo muy agradecido.

    Responder
  2. Aprilio

    En general, las matrices diagonales no conmutan con cualquier matriz. Si D es diagonal, el producto AD multiplica la k-ésima columna de A por el K-ésimo elemento de la diagonal de D. Por otro lado, DA multiplica la k-ésima fila de A por el K-ésimo elemento de la diagonal de D. Sin embargo, sí es cierto que dos matrices diagonales cuales quiera cuyos elementos están en un cuerpo conmutan, pues dicho producto es una matriz diagonal cuyos elementos diagonales son los productos de los correspondientes elementos diagonales de los factores, y en un cuerpo se cumple la propiedad conmutativa del producto.

    Responder

Deja un comentario

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *

Ir arriba