Matriz Antihermitiana (o Antihermítica)

En esta página verás qué es una matriz antihermitiana, también llamada como matriz antihermítica. Encontrarás ejemplos de matrices antihermitianas, todas sus propiedades y la forma que tienen este tipo de matrices complejas cuadradas. Finalmente, hallarás la explicación de cómo descomponer cualquier matriz compleja en la suma de una matriz antihermitiana más otra matriz hermitiana.

¿Qué es una matriz antihermitiana o antihermítica?

Como curiosidad, a este tipo de matriz se le dice de esta manera porque cumple la condición opuesta a la matriz hermítica, cuyo nombre proviene del importante matemático francés Charles Hermite, un profesor e investigador de matemáticas del siglo XIX que hizo importantes estudios especialmente en el campo del álgebra lineal.

Ejemplos de matrices antihermitianas

Una vez vista la definición de matriz antihermitiana (o matriz antihermítica) vamos a ver algunos ejemplos de matrices antihermitianas de varias dimensiones:

Ejemplo de matriz antihermitiana de orden 2×2

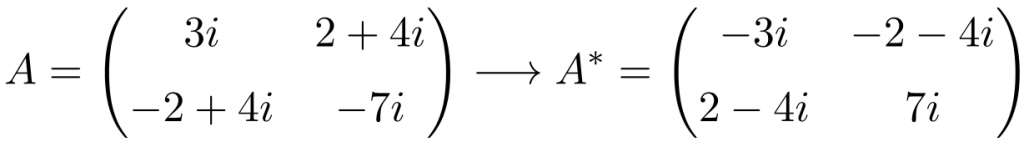
Ejemplo de matriz antihermitiana de dimensión 3×3

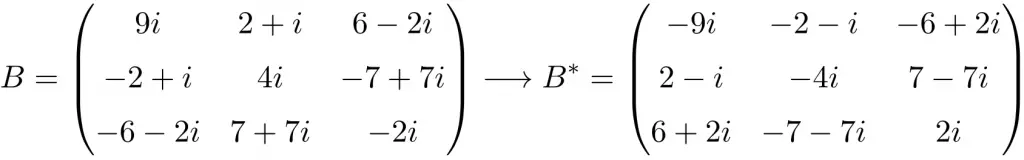
Ejemplo de matriz antihermitiana de tamaño 4×4

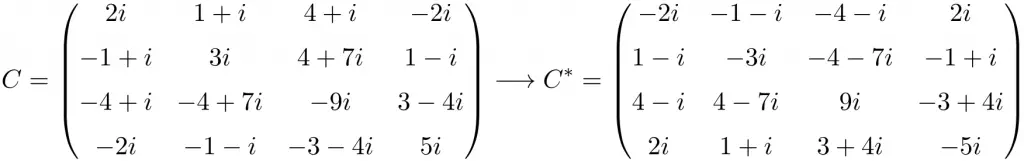
Como puedes ver, las matrices A, B y C son antihermitianas porque la matriz transpuesta conjugada de cada una es igual a la propia matriz pero con todos los elementos cambiados de signo.

Estructura de una matriz antihermitiana

Si te has fijado en los ejemplos de antes, las matrices antihermitianas siempre tienen una misma estructura: están formadas por números imaginarios (sin parte real) en la diagonal principal, y el elemento complejo situado en la i-ésima fila y la j-ésima columna debe tener la misma parte imaginaria y la misma parte real pero cambiada de signo que el elemento de la j-ésima fila y la i-ésima columna.

Aunque escrito puede parecer un poco complicado, seguro que se entiende mejor mediante el siguiente ejemplo:

Estructura de una matriz antihermítica de dimensión 2×2

Como ves, los elementos de la diagonal principal de una matriz antihermitiana son totalmente imaginarios y los elementos de la diagonal secundaria tienen la misma parte imaginaria y la parte real cambiada de signo.

Por lo tanto, la parte real de una matriz antihermitiana debe ser antisimétrica y la parte imaginaria simétrica.

Propiedades de la matriz antihermitiana

Ahora pasamos a ver cuáles son las propiedades de este tipo de matriz compleja cuadrada:

• Toda matriz antihermítica es un ejemplo de matriz normal. Aunque no todas las matrices normales son matrices antihermíticas.

• Cualquier matriz antihermitiana es diagonalizable. Además, la matriz diagonal obtenida solo contiene elementos puramente imaginarios.

• Por lo tanto, los valores propios (o autovalores) de una matriz antihermitiana siempre son números imaginarios.

• Asimismo, los vectores propios (o autovectores) de distintos valores propios de una matriz antihermitiana son ortogonales.

• Una matriz de números reales, es decir que ningún elemento tiene parte imaginaria, es antihermítica si, y solo si, es una matriz antisimetrica.

• Una matriz antihermitiana se puede expresar como la suma de una matriz antisimétrica real más una matriz simétrica imaginaria.

• La suma (o resta) de dos matrices antihermitianas es igual a otra matriz antihermitiana.

• El resultado del producto de una matriz antihermitiana por un escalar es otra matriz antihermitiana si el escalar es un número real.

• La potencia de una matriz antihermitiana es igual a una matriz antihermitiana si el exponente es impar, en cambio, si está elevada a un exponente par el resultado será una matriz hermitiana.

• Si es una matriz antihermítica, entonces el producto es una matriz hermítica.

Descomposición de una matriz compleja en una matriz antihermitiana y una hermitiana

Cualquier matriz que contenga números complejos se puede descomponer en la suma de una matriz antihermitiana más otra matriz hermitiana. Pero para ello debemos conocer las siguientes características de estos tipos de matrices:

• La suma de una matriz compleja cuadrada más su conjugada traspuesta equivale a una matriz hermitiana (o hermítica):

• La diferencia entre una matriz compleja cuadrada y su conjugada traspuesta es igual a una matriz antihermitiana:

• Por lo tanto, todas las matrices complejas se pueden descomponer en la suma de una matriz hermitiana y otra antihermitiana. Este teorema se conoce como descomposición de Teoplitz:

Donde C es la matriz compleja que queremos descomponer, C* su conjugada traspuesta, y por último A y B son las matrices hermitiana y antihermitiana respectivamente en las que se descompone la matriz C.