¿Qué es una matriz Normal? (ejemplos, propiedades y ejercicios)

En esta página verás qué es una matriz normal así como ejemplos de matrices normales. Además, encontrarás las propiedades de este tipo de matrices y ejercicios resueltos paso a paso.

Sumario

1. ¿Qué es una matriz normal?

2. Ejemplos de matrices normales

2.1. Ejemplo con números complejos

2.2. Ejemplo con números reales

3. Propiedades de las matrices normales

4. Ejercicios resueltos de matrices normales

¿Qué es una matriz normal?

La definición de matriz normal es la siguiente:

Una matriz normal es una matriz compleja que multiplicada por su matriz traspuesta conjugada es igual al producto de la traspuesta conjugada por ella misma.

$A\cdot A^*=A^*\cdot A$

Donde $A^*$ es la matriz traspuesta conjugada de $A$ .

Sin embargo, si se tratan de matrices con números reales, la condición anterior es lo mismo que decir que una matriz conmuta con su traspuesta, es decir:

$A\cdot A^t=A^t\cdot A$

Porque, evidentemente, la matriz traspuesta conjugada de una matriz real es simplemente la matriz traspuesta (o transpuesta).

Ejemplos de matrices normales

Ejemplo con números complejos

La siguiente matriz cuadrada compleja de dimensión 2×2 es normal:

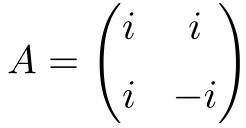
ejemplo de matriz normal con numeros complejos de dimension 2x2

A continuación se adjunta la demostración de su normalidad:

$\displaystyle A\cdot A^* = \begin{pmatrix} i & i \\[1.1ex] i & -i \end{pmatrix} \cdot \begin{pmatrix} -i & -i \\[1.1ex] -i & i \end{pmatrix} =\begin{pmatrix} 2 & 0 \\[1.1ex] 0 & 2 \end{pmatrix}$

$\displaystyle A^*\cdot A = \begin{pmatrix} -i & -i \\[1.1ex] -i & i \end{pmatrix}\cdot \begin{pmatrix} i & i \\[1.1ex] i & -i \end{pmatrix} = \begin{pmatrix} 2 & 0 \\[1.1ex] 0 & 2 \end{pmatrix}$

Ejemplo con números reales

La siguiente matriz cuadrada con números reales de orden 2 también es normal:

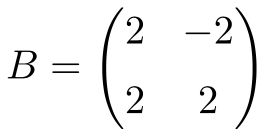
ejemplo de matriz normal con numeros reales de dimension 2x2

En este caso, como únicamente tiene números reales, para demostrar que es normal tan solo debemos comprobar que la matriz es conmutable con su traspuesta:

$\displaystyle B\cdot B^t = \begin{pmatrix} 2 & -2 \\[1.1ex] 2 & 2 \end{pmatrix} \cdot \begin{pmatrix} 2 & 2 \\[1.1ex] -2 & 2 \end{pmatrix} =\begin{pmatrix} 8 & 0 \\[1.1ex] 0 & 8 \end{pmatrix}$

$\displaystyle B^t\cdot B =\begin{pmatrix} 2 & 2 \\[1.1ex] -2 & 2 \end{pmatrix}\cdot \begin{pmatrix} 2 & -2 \\[1.1ex] 2 & 2 \end{pmatrix} =\begin{pmatrix} 8 & 0 \\[1.1ex] 0 & 8 \end{pmatrix}$

Propiedades de las matrices normales

Las matrices normales poseen las siguientes características:

Todas las matrices normales son matrices diagonalizables.

Toda matriz unitaria es también una matriz normal.

Del mismo modo, una matriz hermitiana es una matriz normal.

Igualmente, una matriz antihermítica es una matriz normal.

Si A es una matriz normal, los valores propios (o autovalores) de la matriz traspuesta conjugada A* son los valores propios de A conjugados.

$\displaystyle A=\begin{pmatrix}2i&-1+i\\[1.1ex] 1+i&i\end{pmatrix} \longrightarrow \ \lambda_{A,1} = 0 \ ; \ \lambda_{A,2} = +3i$

$\displaystyle A^*=\begin{pmatrix}-2i&1-i\\[1.1ex] -1-i&-i\end{pmatrix} \longrightarrow \ \lambda_{A^*,1} = 0 \ ; \ \lambda_{A^*,2} = -3i$

En las matrices normales, los vectores propios (o autovectores) asociados a valores propios diferentes son ortogonales.

Si una matriz está compuesta únicamente por números reales y es simétrica, es una matriz normal a la vez.

De igual modo, una matriz real antisimétrica también es una matriz normal.

Por último, cualquier matriz ortogonal formada por números reales también es una matriz normal.

Ejercicios resueltos de matrices normales

Ejercicio 1

Comprueba que la siguiente matriz compleja de dimensión 2×2 es normal:

$\displaystyle A=\begin{pmatrix}1&2+3i\\[1.1ex] 2+3i&1\end{pmatrix}$

Ver solución

Para demostrar que la matriz es normal primero debemos calcular su traspuesta conjugada:

$\displaystyle A^*=\begin{pmatrix}1&2-3i\\[1.1ex] 2-3i&1\end{pmatrix}$

Y ahora hacemos la comprobación multiplicando en los dos sentidos posibles la matriz A por la matriz A*:

$\displaystyle A\cdot A^* = \begin{pmatrix}1&2+3i\\[1.1ex] 2+3i&1\end{pmatrix}\cdot \begin{pmatrix}1&2-3i\\[1.1ex] 2-3i&1\end{pmatrix} = \begin{pmatrix}14&4\\[1.1ex] 4&14\end{pmatrix}$

$\displaystyle A^*\cdot A =\begin{pmatrix}1&2-3i\\[1.1ex] 2-3i&1\end{pmatrix}\cdot \begin{pmatrix}1&2+3i\\[1.1ex] 2+3i&1\end{pmatrix} = \begin{pmatrix}14&4\\[1.1ex] 4&14\end{pmatrix}$

El resultado de ambas multiplicaciones es igual, por lo tanto, la matriz A es normal.

Ejercicio 2

Demuestra que la siguiente matriz real de tamaño 2×2 es normal:

$\displaystyle A=\begin{pmatrix}3&5\\[1.1ex] -5&3\end{pmatrix}$

Ver solución

Como en este caso se trata de un entorno con únicamente números reales, es suficiente comprobar que el producto matricial entre la matriz A y su traspuesta da el mismo resultado independientemente del sentido de la multiplicación:

$\displaystyle A\cdot A^t = \begin{pmatrix}3&5\\[1.1ex] -5&3\end{pmatrix}\cdot \begin{pmatrix}3&-5\\[1.1ex] 5&3\end{pmatrix} = \begin{pmatrix}34&0\\[1.1ex] 0&34\end{pmatrix}$

$\displaystyle A^t\cdot A = \begin{pmatrix}3&-5\\[1.1ex] 5&3\end{pmatrix}\cdot \begin{pmatrix}3&5\\[1.1ex] -5&3\end{pmatrix} = \begin{pmatrix}34&0\\[1.1ex] 0&34\end{pmatrix}$

El resultado de ambos productos es igual, por lo que la matriz A es normal.

Ejercicio 3

Determina si la siguiente matriz de números complejos de orden 2 es normal:

$\displaystyle A=\begin{pmatrix}4i&-1+i\\[1.1ex] 1-i&4i\end{pmatrix}$

Ver solución

Para comprobar que la matriz es normal primero debemos calcular su traspuesta conjugada:

$\displaystyle A^*=\begin{pmatrix}-4i&1+i\\[1.1ex] -1-i&-4i\end{pmatrix}$

Y ahora comprobamos si la matriz A y su traspuesta conjugada son conmutables:

$\displaystyle A\cdot A^* = \begin{pmatrix}4i&-1+i\\[1.1ex] 1-i&4i\end{pmatrix}\cdot \begin{pmatrix}-4i&1+i\\[1.1ex] -1-i&-4i\end{pmatrix} = \begin{pmatrix}18&8i\\[1.1ex] -8i&18\end{pmatrix}$

$\displaystyle A^*\cdot A =\begin{pmatrix}-4i&1+i\\[1.1ex] -1-i&-4i\end{pmatrix}\cdot \begin{pmatrix}4i&-1+i\\[1.1ex] 1-i&4i\end{pmatrix} = \begin{pmatrix}18&8i\\[1.1ex] -8i&18\end{pmatrix}$

El resultado de ambas multiplicaciones es igual, de manera que la matriz A es normal.

Ejercicio 4

Verifica que la siguiente matriz real de dimensión 3×3 es normal:

$\displaystyle A=\begin{pmatrix} -1&1&0\\[1.1ex] 0&-1&1\\[1.1ex] 1&0&-1\end{pmatrix}$

Ver solución

Como la matriz está totalmente compuesta por elementos reales, es suficiente comprobar que el producto matricial entre la matriz A y su traspuesta es independiente del sentido de la multiplicación:

$\displaystyle A\cdot A^t = \begin{pmatrix} -1&1&0\\[1.1ex] 0&-1&1\\[1.1ex] 1&0&-1\end{pmatrix} \cdot\begin{pmatrix}-1&0&1\\[1.1ex] 1&-1&0\\[1.1ex] 0&1&-1\end{pmatrix}=\begin{pmatrix}2&-1&-1\\[1.1ex] -1&2&-1\\[1.1ex] -1&-1&2\end{pmatrix}$

$\displaystyle A^t\cdot A =\begin{pmatrix}-1&0&1\\[1.1ex] 1&-1&0\\[1.1ex] 0&1&-1\end{pmatrix}\cdot \begin{pmatrix} -1&1&0\\[1.1ex] 0&-1&1\\[1.1ex] 1&0&-1\end{pmatrix}=\begin{pmatrix}2&-1&-1\\[1.1ex] -1&2&-1\\[1.1ex] -1&-1&2\end{pmatrix}$

El resultado de ambos productos es igual, de modo que la matriz A es normal.

Ejercicio 5

Determina si la siguiente matriz compleja de orden 3×3 es normal:

$\displaystyle A=\begin{pmatrix}4&3-2i & 5i \\[1.1ex] 3+2i & 0 & -1-3i \\[1.1ex] -5i & -1+3i & 1\end{pmatrix}$

Ver solución

En primer lugar, calculamos la traspuesta conjugada de la matriz:

$\displaystyle A^*=\begin{pmatrix}4&3-2i & 5i \\[1.1ex] 3+2i & 0 & -1-3i \\[1.1ex] -5i & -1+3i & 1\end{pmatrix}$

Ahora deberíamos hacer las multiplicaciones matriciales entre la matriz A y su traspuesta conjugada en los dos sentidos posibles. Sin embargo, la matriz traspuesta conjugada de A es igual a la propia matriz A, por tanto, esta es una matriz hermitiana. Y, en consecuencia, por las propiedades de las matrices normales se deduce que A es una matriz normal, porque cualquier matriz hermitiana es una matriz normal.

Matriz normal

¿Qué es una matriz normal?

Ejemplos de matrices normales

Ejemplo con números complejos

Ejemplo con números reales

Propiedades de las matrices normales

Ejercicios resueltos de matrices normales

Ejercicio 1

Ejercicio 2

Ejercicio 3

Ejercicio 4

Ejercicio 5

Deja un comentario Cancelar respuesta