Matriz Unitaria

En esta página te explicamos qué es la matriz unitaria y, además, lo ejemplificamos con varios ejercicios para que se entienda completamente. También encontrarás cuáles son todas las propiedades de este tipo de matriz tan importante para el álgebra lineal.

Sumario
1. ¿Qué es una matriz unitaria?
2. Ejemplos de matrices unitarias
2.1. Ejemplo de matriz unitaria de dimensión 2×2
2.2. Ejemplo de una matriz diagonal unitaria
3. Propiedades de una matriz unitaria

¿Qué es una matriz unitaria?

La definición de matriz unitaria es la siguiente:

Una matriz unitaria es una matriz compleja que multiplicada por su matriz transpuesta conjugada es igual a la matriz Identidad. Es decir, se cumple la siguiente condición:

U\cdot U^* = U^* \cdot U =I

Donde U es una matriz unitaria y U^* su traspuesta conjugada.

Por lo tanto, esta condición implica que la inversa de una matriz unitaria es su transpuesta conjugada, porque, según la definición de matriz inversa, una matriz es inversa de otra si su producto es equivalente a la matriz Identidad.

\left.\begin{array}{c} U \cdot U^* =I \\[2ex] U \cdot U^{-1} = I\end{array} \right\} \longrightarrow \ U^*=U^{-1}

Por lo que una matriz unitaria siempre será una matriz regular o no degenerada, ya que siempre tendrá inversa.

Por otro lado, el análogo de una matriz unitaria en un entorno con números reales es la matriz ortogonal, y en dicho caso se cumple que la matriz unitaria multiplicada por su traspuesta es igual a la matriz Identidad.

U\cdot U^t = U^t \cdot U =I

De modo que en este caso la matriz inversa de U sería directamente su matriz traspuesta (o transpuesta).

Ejemplos de matrices unitarias

Ejemplo de matriz unitaria de dimensión 2×2

Una vez visto el concepto de matriz unitaria, vamos a ver un ejemplo de una matriz unitaria 2×2 para acabarlo de entender del todo:

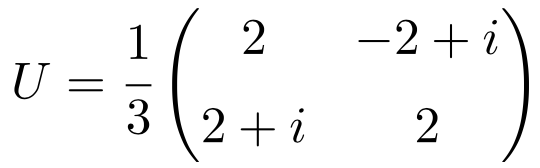
ejemplo de matriz unitaria de dimension 2x2

Esta matriz es unitaria debido a que la multiplicación de ella misma por su matriz conjugada da como resultado la matriz Identidad (o Unidad):

\displaystyle U\cdot U^*=\cfrac{1}{3} \begin{pmatrix} 2 & -2+i \\[1.1ex] 2+i & 2 \end{pmatrix}\cdot \cfrac{1}{3} \begin{pmatrix} 2 & 2-i \\[1.1ex] -2-i & 2 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}

Y, como hemos visto antes, cualquier matriz unitaria es conmutable con su traspuesta conjugada:

\displaystyle U^*\cdot U=\cfrac{1}{3} \begin{pmatrix} 2 & 2-i \\[1.1ex] -2-i & 2 \end{pmatrix}\cdot \cfrac{1}{3} \begin{pmatrix} 2 & -2+i \\[1.1ex] 2+i & 2 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}

Ejemplo de una matriz diagonal unitaria

La matriz diagonal compuesta solamente por el número complejo i también es un ejemplo de matriz unitaria, independientemente de la dimensión de la matriz. A continuación tienes un ejercicio resuelto ejemplificando esto con un matriz unitaria de dimensión 3×3:

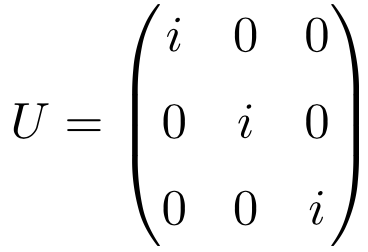
ejemplo de matriz unitaria de dimensión 3x3

Fíjate que si resolvemos el producto de la matriz por su traspuesta conjugada da como solución la matriz Identidad:

\displaystyle U\cdot U^* =\begin{pmatrix} i & 0 & 0 \\[1.1ex] 0 & i & 0 \\[1.1ex] 0& 0 & i \end{pmatrix}\cdot \begin{pmatrix} -i & 0 & 0 \\[1.1ex] 0 & -i & 0 \\[1.1ex] 0& 0 & -i \end{pmatrix}=\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0& 0 & 1 \end{pmatrix}

Y lo mismo sucede si multiplicamos las matrices en el sentido invertido:

\displaystyle U^*\cdot U =\begin{pmatrix} -i & 0 & 0 \\[1.1ex] 0 & -i & 0 \\[1.1ex] 0& 0 & -i \end{pmatrix}\cdot \begin{pmatrix} i & 0 & 0 \\[1.1ex] 0 & i & 0 \\[1.1ex] 0& 0 & i \end{pmatrix}=\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0& 0 & 1 \end{pmatrix}

La característica de esta matriz es que sirve como ejemplo de matriz unitaria de cualquier dimensión, ya que siempre que la matriz esté formada por el número imaginario i en la diagonal principal y el resto de elementos sean cero (0) será una matriz unitaria.

Propiedades de una matriz unitaria

Las propiedades de las matrices unitarias son las siguientes:

  • Evidentemente, toda matriz unitaria es una matriz normal. Aunque no todas las matrices normales son matrices unitarias.
  • Todas la matrices unitarias son diagonalizables, es decir, se pueden transformar en matrices diagonales.
  • El valor absoluto del determinante de una matriz unitaria siempre es igual a 1.

\begin{vmatrix} det(U) \end{vmatrix} = 1

  • Para cualquier número entero n, el conjunto de todas las matrices unitarias n\times n junto con la operación producto matricial forman un grupo, llamado grupo unitario.
  • De manera que la multiplicación de dos matrices unitarias del mismo orden da como resultado otra matriz unitaria.
  • El módulo de todos los valores propios (o autovalores) de una matriz unitaria siempre es igual a 1.

\begin{vmatrix} \lambda \end{vmatrix} = 1

  • Los espacios propios de este tipo de matrices son ortogonales.

Deja un comentario

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *

Ir arriba